# init repo notebook
!git clone https://github.com/rramosp/ppdl.git > /dev/null 2> /dev/null
!mv -n ppdl/content/init.py ppdl/content/local . 2> /dev/null
!pip install -r ppdl/content/requirements.txt > /dev/null
Discrete distributions#
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import pandas as pd
from rlxutils import subplots
import sys
import init
%matplotlib inline
Discrete (or categorical) distributions#
we will have a joint distribute distritbution of two variables, in the example below these are \(edad\) and \(barrio\).
each variable make take any value from a FINITE set. Observe that \(edad\) is discrete because its value comes binned into age groups.
the possible values for each variable might be sortable in a meaningful way or not. \(edad\) is sortable, \(barrio\) is not, because an alphabetical sorting does not imply any relation.
for instance, that \(edad\)
10-14<25-29represents a true relation of data (younger/older people)but \(barrio\)
Aranjuez<Belendoes NOT represent any true relation between the two neighborhoods. It is somewhat arbitrary.
recall that:
the joint probability is the probability of a value of \(edad\) and a value of \(barrio\) for occurring simultaneously. Answers the question: What is the observed proportion of people with age
10-14and living inBelen.the marginal probability is the probability of a value of one variable irrespective of the outcome of the another variable. Answers the question: What is the observed proportion of people living in \(belen\)?.
the conditional probability is the probability of one event occurring in the presence of a second event. Answers the question: If we only consider people living in \(belen\), what is the observed proportion of people with ages
10-14?
This is the data of people ages and district in Medellin where they live, taken from medata.gov.co
x = pd.read_csv("local/data/proyecciones_de_poblacion_medellin_2017.csv.gz", delimiter=";")
x['grupo_edad'] = x.grupo_edad.str.strip().str.lower()
x = x.rename({"codigo": "barrio", "grupo_edad": "edad"}, axis=1)
x = x.replace("0-4", '00-04').replace('5-9', '05-09').replace('80 y más', '80-')
x = x[x.edad.str.lower().str.strip()!="total"]
x = x[[("Suma" not in i)&("Total" not in i) for i in x.barrio]]
x = x.groupby(["edad", "barrio" ])[['total_2017']].sum().unstack().T.loc['total_2017']
x
| edad | 00-04 | 05-09 | 10-14 | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 | 65-69 | 70-74 | 75-79 | 80- |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| barrio | |||||||||||||||||
| Altavista | 3281 | 3183 | 3538 | 3467 | 3888 | 3861 | 3270 | 2990 | 3270 | 2689 | 1896 | 1107 | 717 | 520 | 421 | 367 | 109 |
| Aranjuez | 10047 | 10206 | 10357 | 10976 | 11936 | 13804 | 13695 | 11557 | 9851 | 11339 | 12631 | 11616 | 8990 | 6352 | 4103 | 2551 | 2904 |
| Belén | 8406 | 9304 | 9695 | 12281 | 14230 | 15365 | 15848 | 14129 | 11069 | 13116 | 16739 | 16754 | 13710 | 10397 | 6893 | 4369 | 5094 |
| Buenos Aires | 6968 | 7288 | 7212 | 8611 | 10025 | 11343 | 11011 | 9835 | 8276 | 9630 | 11503 | 11146 | 8586 | 6071 | 3991 | 2713 | 3046 |
| Castilla | 7844 | 7986 | 8228 | 8743 | 10642 | 12446 | 11560 | 10021 | 9083 | 12129 | 14627 | 12250 | 9130 | 6665 | 4253 | 2652 | 2622 |
| Doce de Octubre | 12714 | 12562 | 12473 | 13301 | 14749 | 15935 | 14512 | 12670 | 11435 | 14508 | 16409 | 14151 | 10555 | 7568 | 4926 | 3150 | 3169 |
| El Poblado | 3666 | 4212 | 4527 | 5353 | 6363 | 8189 | 9540 | 9600 | 8681 | 10461 | 13356 | 13622 | 11246 | 8634 | 5739 | 4086 | 4211 |
| Guayabal | 4175 | 4428 | 4523 | 5268 | 6217 | 7460 | 7620 | 6692 | 5463 | 6768 | 8231 | 7821 | 6743 | 5364 | 3552 | 2546 | 2526 |
| La América | 2439 | 2883 | 3034 | 4091 | 4923 | 6154 | 6775 | 6377 | 5143 | 6418 | 9502 | 10146 | 8779 | 7678 | 5315 | 3393 | 3868 |
| La Candelaria | 3111 | 3453 | 3715 | 4038 | 4557 | 6305 | 7479 | 6949 | 5157 | 5944 | 7206 | 7179 | 6452 | 5097 | 3330 | 2382 | 3304 |
| Laureles - Estadio | 2906 | 3533 | 3910 | 4850 | 5523 | 7946 | 9810 | 9010 | 6861 | 7589 | 10124 | 11632 | 11062 | 9895 | 6966 | 5262 | 5865 |
| Manrique | 11440 | 11314 | 11312 | 11756 | 12422 | 13701 | 12536 | 10458 | 9325 | 11208 | 12622 | 11293 | 8057 | 5460 | 3568 | 2238 | 2360 |
| Palmitas | 474 | 417 | 543 | 609 | 666 | 646 | 505 | 430 | 634 | 611 | 507 | 361 | 233 | 198 | 109 | 87 | 31 |
| Popular | 11799 | 11707 | 11113 | 11056 | 10779 | 10956 | 10037 | 8971 | 7859 | 8280 | 8382 | 6789 | 4860 | 3426 | 2228 | 1589 | 1614 |
| Robledo | 10897 | 11153 | 11142 | 12065 | 13989 | 14847 | 13997 | 12195 | 10244 | 11809 | 13580 | 12245 | 9498 | 6923 | 4467 | 2596 | 2759 |
| San Antonio | 8610 | 8208 | 9796 | 9925 | 11907 | 11737 | 10736 | 9990 | 11105 | 8874 | 6166 | 4119 | 2517 | 1601 | 1102 | 875 | 326 |
| San Cristóbal | 6985 | 6898 | 8400 | 8337 | 9241 | 9375 | 8014 | 7614 | 8303 | 6913 | 4641 | 3257 | 1901 | 1243 | 887 | 780 | 283 |
| San Javier | 9775 | 10642 | 10930 | 11672 | 11885 | 12005 | 11317 | 10307 | 8614 | 8838 | 9205 | 7705 | 5679 | 4049 | 2620 | 1693 | 2239 |
| Santa Cruz | 8789 | 8720 | 8546 | 8891 | 9289 | 9814 | 9039 | 7867 | 6491 | 7037 | 7978 | 6554 | 4581 | 3424 | 2257 | 1471 | 1766 |
| Santa Elena | 1559 | 1491 | 1725 | 1670 | 1785 | 1997 | 1757 | 1495 | 1514 | 1488 | 1077 | 678 | 511 | 353 | 250 | 159 | 50 |
| Villa Hermosa | 9971 | 10346 | 10228 | 11280 | 11901 | 12581 | 11909 | 10075 | 7885 | 7939 | 8694 | 7737 | 6052 | 4552 | 2970 | 1952 | 2470 |
joint distribution#
we turn it into a joint distribution. This is an empirical distribution, because the data was obtained by counting using some method on the real world and not derived or assumed by some analytical procedure or calculation.
xd = x/x.values.sum()
xd
| edad | 00-04 | 05-09 | 10-14 | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 | 65-69 | 70-74 | 75-79 | 80- |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| barrio | |||||||||||||||||
| Altavista | 0.001308 | 0.001269 | 0.001410 | 0.001382 | 0.001550 | 0.001539 | 0.001304 | 0.001192 | 0.001304 | 0.001072 | 0.000756 | 0.000441 | 0.000286 | 0.000207 | 0.000168 | 0.000146 | 0.000043 |
| Aranjuez | 0.004005 | 0.004069 | 0.004129 | 0.004376 | 0.004758 | 0.005503 | 0.005460 | 0.004607 | 0.003927 | 0.004520 | 0.005035 | 0.004631 | 0.003584 | 0.002532 | 0.001636 | 0.001017 | 0.001158 |
| Belén | 0.003351 | 0.003709 | 0.003865 | 0.004896 | 0.005673 | 0.006125 | 0.006318 | 0.005633 | 0.004413 | 0.005229 | 0.006673 | 0.006679 | 0.005466 | 0.004145 | 0.002748 | 0.001742 | 0.002031 |
| Buenos Aires | 0.002778 | 0.002905 | 0.002875 | 0.003433 | 0.003996 | 0.004522 | 0.004390 | 0.003921 | 0.003299 | 0.003839 | 0.004586 | 0.004443 | 0.003423 | 0.002420 | 0.001591 | 0.001082 | 0.001214 |
| Castilla | 0.003127 | 0.003184 | 0.003280 | 0.003485 | 0.004242 | 0.004962 | 0.004608 | 0.003995 | 0.003621 | 0.004835 | 0.005831 | 0.004883 | 0.003640 | 0.002657 | 0.001695 | 0.001057 | 0.001045 |
| Doce de Octubre | 0.005068 | 0.005008 | 0.004972 | 0.005302 | 0.005880 | 0.006353 | 0.005785 | 0.005051 | 0.004559 | 0.005784 | 0.006541 | 0.005641 | 0.004208 | 0.003017 | 0.001964 | 0.001256 | 0.001263 |
| El Poblado | 0.001461 | 0.001679 | 0.001805 | 0.002134 | 0.002537 | 0.003265 | 0.003803 | 0.003827 | 0.003461 | 0.004170 | 0.005324 | 0.005430 | 0.004483 | 0.003442 | 0.002288 | 0.001629 | 0.001679 |
| Guayabal | 0.001664 | 0.001765 | 0.001803 | 0.002100 | 0.002478 | 0.002974 | 0.003038 | 0.002668 | 0.002178 | 0.002698 | 0.003281 | 0.003118 | 0.002688 | 0.002138 | 0.001416 | 0.001015 | 0.001007 |
| La América | 0.000972 | 0.001149 | 0.001210 | 0.001631 | 0.001963 | 0.002453 | 0.002701 | 0.002542 | 0.002050 | 0.002559 | 0.003788 | 0.004045 | 0.003500 | 0.003061 | 0.002119 | 0.001353 | 0.001542 |
| La Candelaria | 0.001240 | 0.001377 | 0.001481 | 0.001610 | 0.001817 | 0.002514 | 0.002982 | 0.002770 | 0.002056 | 0.002370 | 0.002873 | 0.002862 | 0.002572 | 0.002032 | 0.001328 | 0.000950 | 0.001317 |
| Laureles - Estadio | 0.001158 | 0.001408 | 0.001559 | 0.001933 | 0.002202 | 0.003168 | 0.003911 | 0.003592 | 0.002735 | 0.003025 | 0.004036 | 0.004637 | 0.004410 | 0.003945 | 0.002777 | 0.002098 | 0.002338 |
| Manrique | 0.004561 | 0.004510 | 0.004510 | 0.004687 | 0.004952 | 0.005462 | 0.004998 | 0.004169 | 0.003717 | 0.004468 | 0.005032 | 0.004502 | 0.003212 | 0.002177 | 0.001422 | 0.000892 | 0.000941 |
| Palmitas | 0.000189 | 0.000166 | 0.000216 | 0.000243 | 0.000266 | 0.000258 | 0.000201 | 0.000171 | 0.000253 | 0.000244 | 0.000202 | 0.000144 | 0.000093 | 0.000079 | 0.000043 | 0.000035 | 0.000012 |
| Popular | 0.004704 | 0.004667 | 0.004430 | 0.004407 | 0.004297 | 0.004368 | 0.004001 | 0.003576 | 0.003133 | 0.003301 | 0.003342 | 0.002706 | 0.001937 | 0.001366 | 0.000888 | 0.000633 | 0.000643 |
| Robledo | 0.004344 | 0.004446 | 0.004442 | 0.004810 | 0.005577 | 0.005919 | 0.005580 | 0.004862 | 0.004084 | 0.004708 | 0.005414 | 0.004881 | 0.003786 | 0.002760 | 0.001781 | 0.001035 | 0.001100 |
| San Antonio | 0.003432 | 0.003272 | 0.003905 | 0.003957 | 0.004747 | 0.004679 | 0.004280 | 0.003983 | 0.004427 | 0.003538 | 0.002458 | 0.001642 | 0.001003 | 0.000638 | 0.000439 | 0.000349 | 0.000130 |
| San Cristóbal | 0.002785 | 0.002750 | 0.003349 | 0.003324 | 0.003684 | 0.003737 | 0.003195 | 0.003035 | 0.003310 | 0.002756 | 0.001850 | 0.001298 | 0.000758 | 0.000496 | 0.000354 | 0.000311 | 0.000113 |
| San Javier | 0.003897 | 0.004242 | 0.004357 | 0.004653 | 0.004738 | 0.004786 | 0.004512 | 0.004109 | 0.003434 | 0.003523 | 0.003670 | 0.003072 | 0.002264 | 0.001614 | 0.001044 | 0.000675 | 0.000893 |
| Santa Cruz | 0.003504 | 0.003476 | 0.003407 | 0.003544 | 0.003703 | 0.003912 | 0.003603 | 0.003136 | 0.002588 | 0.002805 | 0.003180 | 0.002613 | 0.001826 | 0.001365 | 0.000900 | 0.000586 | 0.000704 |
| Santa Elena | 0.000621 | 0.000594 | 0.000688 | 0.000666 | 0.000712 | 0.000796 | 0.000700 | 0.000596 | 0.000604 | 0.000593 | 0.000429 | 0.000270 | 0.000204 | 0.000141 | 0.000100 | 0.000063 | 0.000020 |
| Villa Hermosa | 0.003975 | 0.004124 | 0.004077 | 0.004497 | 0.004744 | 0.005015 | 0.004748 | 0.004016 | 0.003143 | 0.003165 | 0.003466 | 0.003084 | 0.002413 | 0.001815 | 0.001184 | 0.000778 | 0.000985 |
# it must add up to 1
xd.values.sum()
1.0
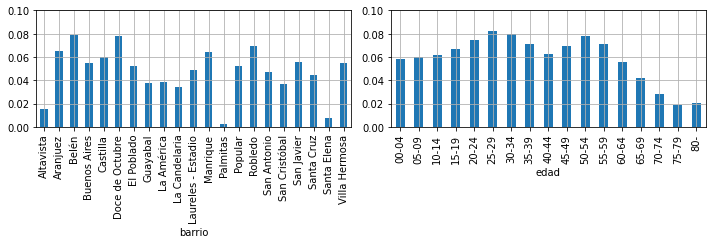
marginal distribution#
This are the TWO marginal distributions, for each one of the variables
dbarrio = xd.sum(axis=1)
dedad = xd.sum(axis=0)
dbarrio.sum(), dedad.sum()
(1.0, 1.0)
for ax,i in subplots(2, usizex=5, usizey=3.5):
if i==0: dbarrio.plot(kind="bar")
if i==1: dedad.plot(kind="bar")
plt.grid()
plt.ylim(0,0.1)
plt.tight_layout()
conditional distribution#
we compute it for one variable with respect to a specific value of the other one.
This is
observe that we obtain it from the join distribution but WE MUST NORMALIZE so we have a true distribution adding up to 1.
This normalization will become very important later on in the course.
# unnormalized conditional
xd.loc['Belén']
edad
00-04 0.003351
05-09 0.003709
10-14 0.003865
15-19 0.004896
20-24 0.005673
25-29 0.006125
30-34 0.006318
35-39 0.005633
40-44 0.004413
45-49 0.005229
50-54 0.006673
55-59 0.006679
60-64 0.005466
65-69 0.004145
70-74 0.002748
75-79 0.001742
80- 0.002031
Name: Belén, dtype: float64
# it does not add up to one
xd.loc['Belén'].sum()
0.07869355283657012
# we normalized it
dbelen = xd.loc['Belén'] / xd.loc['Belén'].sum()
print ("check sum =", dbelen.sum())
dbelen
check sum = 1.0
edad
00-04 0.042584
05-09 0.047133
10-14 0.049114
15-19 0.062214
20-24 0.072087
25-29 0.077837
30-34 0.080284
35-39 0.071576
40-44 0.056074
45-49 0.066444
50-54 0.084798
55-59 0.084874
60-64 0.069453
65-69 0.052670
70-74 0.034919
75-79 0.022133
80- 0.025806
Name: Belén, dtype: float64
dbelen.plot(kind='bar', figsize=(6,2))
plt.grid();
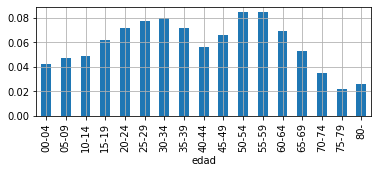
Sometimes we write
without specifying the value of the conditioning variable, but assuming someone has decided upon a certain value. You must pay attention to the context in which this is being used to understand well how to compute or use this conditional distribution.
In fact, for each value of \(barrio\) we have a different distritbuion.
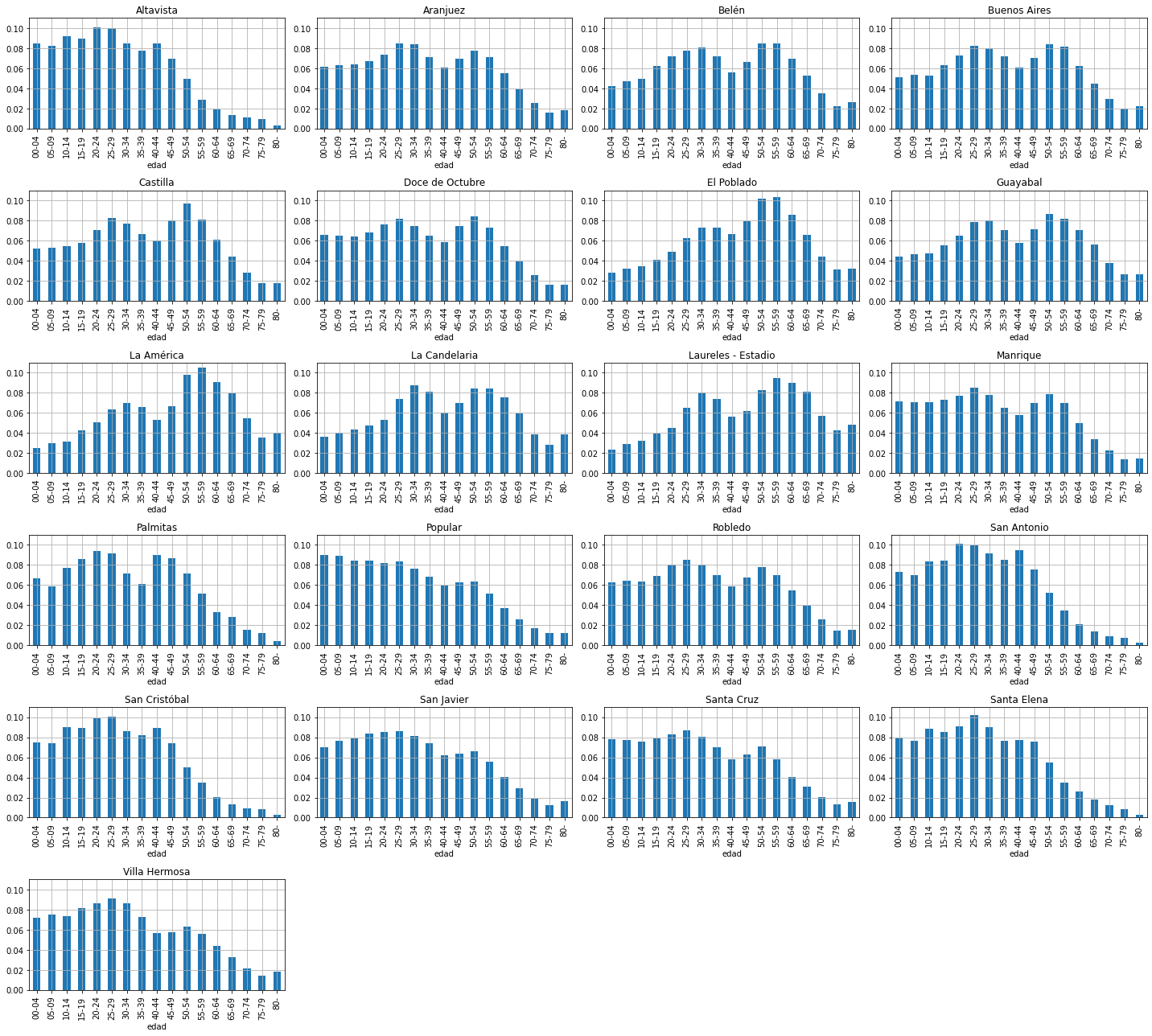
independance#
Observe carefully. If all conditional distributions look the same this suggests that both variables are independant, \(\rightarrow\) knowing something about one does not tell us anything about the other one.
for ax,barrio in subplots(xd.index, usizex=5, usizey=3, n_cols=4):
dmarginal = xd.loc[barrio] / xd.loc[barrio].sum()
dmarginal.plot(kind='bar', ax=ax)
plt.title(barrio)
plt.ylim(0,.11)
plt.grid();
plt.tight_layout()
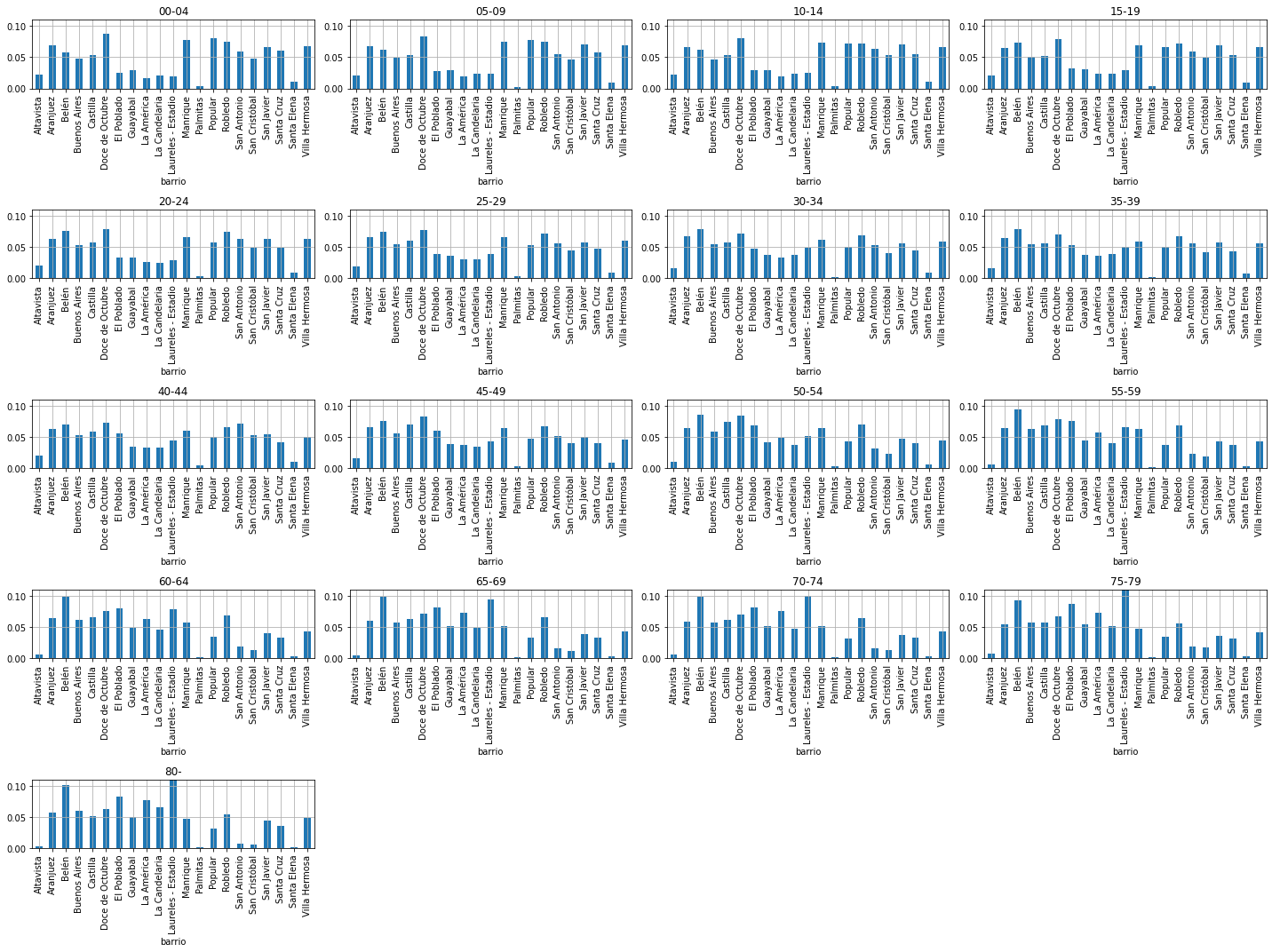
or for each value of \(edad\)
for ax,edad in subplots(xd.columns, usizex=5, usizey=3, n_cols=4):
dmarginal = xd[edad] / xd[edad].sum()
dmarginal.plot(kind='bar', ax=ax)
plt.title(edad)
plt.ylim(0,.11)
plt.grid();
plt.tight_layout()