LAB 11 - KNAPSACK PROBLEM
Contents
LAB 11 - KNAPSACK PROBLEM¶
!wget --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/20192.L3/master/init.py
import init; init.init(force_download=False); init.get_weblink()
import init
from local.lib.rlxmoocapi import submit, session
import inspect
student = session.Session(init.endpoint).login( course_id=init.course_id,
session_id="UDEA",
lab_id="lab_11" )
from IPython.display import Image
Image(filename='local/imgs/ks.jpg')

Tenemos \(n\) objectos numerados del \(0\) a \(n-1\), con un tamaño \(s_i\) y valor \(v_i\) cada uno. Una solución cualquiera del problema es el vector \(X=[x_0, x_2, ..., x_i, ... x_{n-1}]\), en donde \(x_i \in \{0,1\}\) indica si el objecto \(i\) se incluye o no la mochila. Como la mochila tiene un volumen máximo, \(KS_{vol}\) el problema se formula de la siguiente manera:
El vector \(S=[s_0, s_2, ..., s_i, ... s_{n-1}]\) representa los tamaños de todos los objectos y el vector \(V=[v_0, v_2, ..., v_i, ... v_{n-1}]\), los valores.
Fíjate a continuación cómo:
generamos vectores \(S\) y \(V\) aleatorios
generamos soluciones aleatorias
verificamos si las soluciones generadas son válidas
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
n_objects = 10
max_object_value = 100
max_object_volume = 50
KS_volume = 100
object_values = np.random.randint(max_object_value-1, size=n_objects)+1
object_volumes = np.random.randint(max_object_volume-1, size=n_objects)+1
print ("vals ", object_values)
print ("sizes", object_volumes)
def KS_isvalid(solution, object_volumes, KS_volume):
return np.sum(solution*object_volumes)<=KS_volume
for i in range(10):
solution = np.random.randint(2, size=len(object_volumes))
print ("solution", i, solution, KS_isvalid(solution, object_volumes, KS_volume))
vals [45 86 48 32 60 73 27 59 75 71]
sizes [44 6 8 9 25 27 25 25 13 23]
solution 0 [0 1 0 0 1 1 1 1 0 0] False
solution 1 [1 0 1 0 0 0 0 1 0 0] True
solution 2 [0 0 0 0 0 1 1 1 0 0] True
solution 3 [1 0 1 0 1 0 0 0 1 0] True
solution 4 [0 1 1 1 0 1 0 1 0 1] True
solution 5 [1 1 1 0 0 0 0 1 1 1] False
solution 6 [1 1 0 0 1 0 0 0 1 0] True
solution 7 [1 0 1 1 0 0 0 0 0 0] True
solution 8 [0 1 0 1 1 0 1 1 1 0] False
solution 9 [1 1 1 1 1 0 1 1 1 1] False
HAZTE LA SIGUIENTE PREGUNTA ¿Cuál es la probabilidad de que una solución aleatoria sea válida?
Ejercicio 1: Inicialización de la población¶
Crea una función para crear una población de soluciones aleatorias. Ten en cuenta que
TODAS LAS SOLUCIONES HAN DE SER VÁLIDAS.
Si creas soluciones aleatorias y las descartas si no son válidas seguramente tu código tarde mucho en generar la población si la probablidad de que una solución aleatoria sea válida es muy pequeña
Tu código ha de devolver un array numpy de números enteros
Ejecución de ejemplo
n_objects = 20
KS_volume = 50
n_individuals = 10
pop = KS_initialize_population(n_individuals, object_volumes, KS_volume)
print pop
Salida esperada (la población es aleatoria, tu salida probablemente sea distinta)
[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1],
[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
def KS_initialize_population(n_individuals, object_volumes, KS_volume):
##<---- Ingresa tu código aquí ---->
return
Verifica tu código
n_objects = 50
max_object_value = 100
max_object_volume = 50
KS_volume = 50
n_individuals = 100
object_values = np.random.randint(max_object_value-1, size=n_objects)+1
object_volumes = np.random.randint(max_object_volume-1, size=n_objects)+1
pop = KS_initialize_population(n_individuals, object_volumes, KS_volume)
n_invalid = int(np.sum([1 for i in pop if not KS_isvalid(i, object_volumes, KS_volume)]))
print("Hay", n_invalid, "soluciones inválidas de un total de", len(pop), "soluciones")
Ejercicio 2: Función de coste¶
El valor máximo que tendríamos si pudiéramos incluir todos los objetos en la mochila sería \(V_{max}=\sum v_i\). El volumen de los objetos incluidos en una solución \(X\) es \(S(X)=\sum s_i x_i\). El valor de todos los objetos incluidos en una solución es \(V(X)=\sum v_i x_i\)
Crea una función de coste de manera que valores altos de las combinaciones de objetos representen un coste bajo, siempre y cuando no excedan la capacidad de la mochila. Observa que nuestra implementación de GA MINIMIZA un coste y nosotros queremos MAXIMIZAR un valor.
def KS_cost(solution, object_values, object_volumes, KS_volume):
##<-- Ingrese su codigo aqui-->
return
Comprueba tu código. La gráfica generada tiene que tener aproximadamente la siguiente forma:
from IPython.display import Image
Image(filename='local/imgs/kscost.jpg')
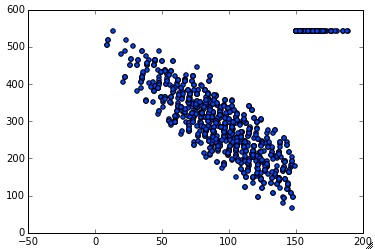
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
n_objects = 10
max_object_value = 100
max_object_volume = 40
KS_volume = 150
n_individuals = 1000
object_values = np.random.randint(max_object_value-1, size=n_objects)+1
object_volumes = np.random.randint(max_object_volume-1, size=n_objects)+1
pop = KS_initialize_population(n_individuals, object_volumes, KS_volume)
pop = np.random.randint(2, size=(n_individuals, len(object_volumes)))
vols = [np.sum(i*object_volumes) for i in pop]
costs = [KS_cost(i, object_values, object_volumes, KS_volume) for i in pop]
plt.scatter(vols, costs)
Ejercicio 3: Función de mutación¶
Crea una función de mutación que, con probabilidad \(mutation\_prob\) genere una mutación VALIDA de un bit de una solución.
Ejemplo de ejecución:
sol = np.array([0 0 0 0 1 0 1 1 0 0])
print KS_mutate(pop[1], 0.9, object_volumes, KS_volume)
Salida esperada (sujeto a procesos aleatorios):
> [0 0 0 0 1 0 1 0 0 0]
def KS_isvalid(solution, object_volumes, KS_volume):
import numpy as np
return np.sum(solution*object_volumes)<=KS_volume
def KS_mutate(solution, mutation_prob, object_volumes, KS_volume):
import numpy as np
## <-- Ingrese su código aquí -->
return solution
Comprueba tu código
object_values = np.array([22, 19, 49, 32, 66, 86, 51, 94, 33, 33])
object_volumes = np.array([ 6, 36, 8, 14, 12, 19, 27, 4, 15, 4])
KS_volume = 150
pop = np.array([[0, 1, 1, 0, 0, 1, 0, 1, 0, 1],
[1, 1, 0, 1, 1, 0, 0, 1, 1, 1],
[1, 0, 0, 1, 1, 1, 1, 0, 0, 1],
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
mutation_prob = 0.1
print ("original mutada diferencia")
for i in pop:
m = KS_mutate(i, mutation_prob, object_volumes, KS_volume)
print((m, i, np.sum((m-i)**2)))
Ya está! Usaremos la siguiente función de crossover¶
def KS_cross_over(solution1, solution2):
l = len(solution1)
cstart = np.random.randint(l)
cend = np.random.randint(l-cstart)+cstart+1
r = np.zeros(l).astype(int)
r[:cstart] = solution1[:cstart]
r[cstart:cend] = solution2[cstart:cend]
r[cend:] = solution1[cend:]
return r
Creamos un problema KS con volúmenes y valores para objectos¶
##%run utils/ga.py
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
n_objects = 50
KS_volume = 100
mutation_prob = 0.1
crossover_prob = 0.5
object_values = np.array([36, 20, 47, 53, 55, 46, 48, 66, 1, 6, 13, 59, 95, 7, 54, 32, 76, 63, 76, 19, 2, 17, 16, 12, 78,
67, 44, 20, 41, 26, 24, 68, 55, 53, 35, 49, 46, 46, 16, 64, 41, 27, 8, 30, 76, 92, 85, 81, 84, 98])
object_volumes = np.array([ 8, 47, 16, 8, 41, 11, 45, 34, 26, 48, 16, 8, 10, 13, 28, 6, 7, 11, 8, 27, 44, 30, 25, 23, 45,
3, 12, 12, 23, 3, 37, 10, 47, 46, 27, 10, 30, 8, 2, 47, 4, 44, 43, 37, 22, 20, 1, 17, 42, 27])
print ("total volume of objects", np.sum(object_volumes))
print ("knapsack max volume ", KS_volume)
print ("total value of objects ", np.sum(object_values))
print (object_values)
print (object_volumes)
Y vemos cómo se comporta con distintos valores de las probabilidades de mutación y crossover¶
Deberemos de observar cómo el problema está dominado por la probabilidad de mutación
r = run_ga(pop_size=100,
init_population_function = lambda x: KS_initialize_population(x, object_volumes, KS_volume),
mutation_function = lambda x,y: KS_mutate(x, y, object_volumes, KS_volume),
crossover_function = KS_cross_over,
cost_function = lambda x: sKS_cost(x, object_values, object_volumes, KS_volume),
crossover_prob = 0.5,
mutation_prob = 0.5,
n_iters = 100)
best, best_costs, means, stds = r
print ("best knapsack is", best, "cost", np.min(best_costs), "value", np.sum(best*object_values), "volume", np.sum(best*object_volumes))
plot_evolution(best_costs, means, stds)
import PS11_01 as st1
import PS11_02 as st2
import PS11_03 as st3
r = run_ga(pop_size=100,
init_population_function = lambda x: st1.KS_initialize_population(x, object_volumes, KS_volume),
mutation_function = lambda x,y: st3.KS_mutate(x, y, object_volumes, KS_volume),
crossover_function = KS_cross_over,
cost_function = lambda x: st2.KS_cost(x, object_values, object_volumes, KS_volume),
crossover_prob = 0.9,
mutation_prob = 0.9,
n_iters = 400)
best, best_costs, means, stds = r
print ("best knapsack is", best, "cost", np.min(best_costs), "value", np.sum(best*object_values), "volume", np.sum(best*object_volumes))
plot_evolution(best_costs, means, stds)
r = run_ga(pop_size=100,
init_population_function = lambda x: KS_initialize_population(x, object_volumes, KS_volume),
mutation_function = lambda x,y: KS_mutate(x, y, object_volumes, KS_volume),
crossover_function = KS_cross_over,
cost_function = lambda x: KS_cost(x, object_values, object_volumes, KS_volume),
crossover_prob = 0.1,
mutation_prob = 0.1,
n_iters = 200)
best, best_costs, means, stds = r
print ("best knapsack is", best, "cost", np.min(best_costs), "value", np.sum(best*object_values), "volume", np.sum(best*object_volumes))
plot_evolution(best_costs, means, stds)
r = run_ga(pop_size=100,
init_population_function = lambda x: KS_initialize_population(x, object_volumes, KS_volume),
mutation_function = lambda x,y: KS_mutate(x, y, object_volumes, KS_volume),
crossover_function = KS_cross_over,
cost_function = lambda x: KS_cost(x, object_values, object_volumes, KS_volume),
crossover_prob = 0.1,
mutation_prob = 1.0,
n_iters = 200)
best, best_costs, means, stds = r
print ("best knapsack is", best, "cost", np.min(best_costs), "value", np.sum(best*object_values), "volume", np.sum(best*object_volumes))
plot_evolution(best_costs, means, stds)