Grafos
Contents
!wget -nc --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/introalgs.v1/main/content/init.py
import init; init.init(force_download=False);
Grafos¶
Objetivo del módulo¶
Conocer la estructura grafo, la forma como se clasifican, la terminología usada en dicha estructura y la forma de representarla dentro de un computador.
## Preguntas
¿Qué es un grafo?
¿Qué es un grafo dirigido?
¿Qué es un grafo no dirigido?
¿En qué consiste la relación de adyacencia?
¿En qué consiste la relación de incidencia?
¿Cuál es el grado de un vértice?
¿Qué es el grado entrante?
¿Qué es el grado saliente?
¿Qué es una trayectoria?
¿Cuál es la longitud de una trayectoria?
¿Qué es una trayectoria simple?
¿Qué es un ciclo?
¿Qué es un grafo conectado?
¿Qué es un grafo completo?
Introducción¶
Introducción Trataremos en este módulo los conceptos básicos sobre grafos. Los grafos son estructuras ampliamente utilizadas en el modelaje de muchas situaciones que se presentan en la vida real. Un grafo se puede utilizar para representar el pensum de un programa, la secuencia de actividades para construir un edificio, los vuelos de una aerolínea, el sistema vial de una ciudad, una red de computadoras, etc.
Definición: Un grafo consta de:
Un conjunto finito de vértices.
Un conjunto de pares de vértices llamados lados.
Por ejemplo:
from IPython.display import Image
Image(filename='local/imgs/grafos.jpg', width=700)
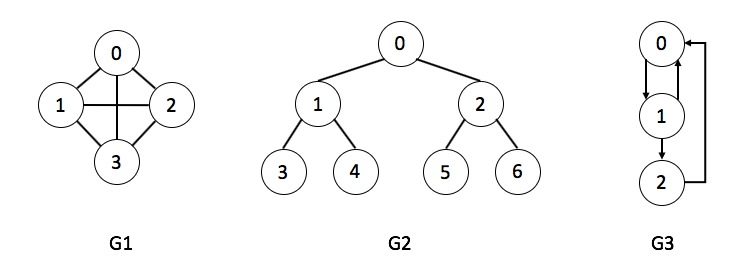
Los conjuntos de vértices y lados para cada uno de los grafos de la figura son:
Grafo G1:
\(V = \{0, 1, 2, 3\}\)
\(E = \{(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)\}\)
Grafo G2
\(V = \{0, 1, 2, 3, 4, 5, 6\}\)
\(E = \{(0,1), (0,2), (1,3), (1,4), (2,5), (2,6)\}\)
Grafo *G3
\(V = \{0, 1, 2\}\)
\(E = \{<0, 1>, <1, 0>, <1, 2>, <2, 0>\}\)
Tipos de grafos¶
Grafos no Dirigidos: son aquellos en los cuales los lados no están orientados, como en los grafos G1 y G2. Cuando se trata de grafos no dirigidos cada pareja de vértices se representa entre paréntesis. El orden de los vértices que definen un lado no es relevante, es decir el lado \((V_i, V_j)\) es exactamente lo mismo que el lado \((V_j, V_i)\)
Grafos Dirigidos: Son aquellos grafos en los cuales los lados están orientados como en el grafo G3. La pareja de vértices que representa un lado se escribe entre ángulos. La orientación del lado depende del orden en que escriba la pareja de vértices. Es decir, el lado \(<V_i, V_j>\) es diferente del lado \(<V_j, V_i>\).
Cuando se trata de un grafo dirigido, cada vértice de un lado se diferencia así:
\(<V_i, V_j>\):
\(V_i\) = cola del lado
\(V_j\) = cabeza del lado
Terminología¶
Dos vértices son adyacentes si conforman un lado.
En el grafo G1 los vértices 0 y 1 son adyacentes, también lo son los vértices 1 y 2.
Para grafos dirigidos la relación de adyacencia se discrimina así: Si tenemos el lado \(<V_i, V_j>\) se dice que \(V_i\) es adyacente hacia \(V_j\) y que \(V_j\) es adyacente desde \(V_i\).
El lado formado por dos vértices es incidente sobre ellos.
Grado de un Vértice: Es el número de lados incidentes sobre él. Para el grafo G1 el grado del vértice 0 es 3. Para el grafo G2 el vértice 3 tiene grado 1 y el vértice 2 tiene grado 3. Para el grafo G3 el vértice 1 tiene grado 3.
Para grafos Dirigidos hay que diferenciar entre grado entrante y grado saliente.
Grado entrante es el número de lados que llegan al vértice y grado saliente es el número de lados que salen del vértice.
Para el grafo G3 el vértice 0 tiene: grado entrante = 2 y grado saliente = 1
En grafos dirigidos el grado total es la suma del grado entrante más el grado saliente.
Trayectoria: Son los vértices por los cuales hay que pasar para ir desde un vértice i hacia un vértice j. Por ejemplo en el grafo G2 para ir desde el vértice 3 hacia el 5, la trayectoria es:
3, 1, 0, 2, 5 {1}
Para que una trayectoria sea válida la condición es que los lados sobre la trayectoria existan en el conjunto de lados que define el grafo. En nuestro ejemplo, los lados definidos en la trayectoria son los lados (3,1), (1,0), (0,2) y (2,5). Todos esos lados existen en el conjunto de lados que definen el grafo G2, por tanto dicha trayectoria es válida.
Si tuviéramos otra trayectoria:
3, 1, 2, 5
Los lados definidos en ella son: (3, 1), (1, 2) y (1, 5). Si observamos el conjunto de lados que define el grafo G2, allí no se encuentra definido el lado (1, 2), por consiguiente, la trayectoria presentada aquí no es válida.
Longitud de una trayectoria: Es el número de lados en ella. En el ejemplo de la trayectoria {1}, la cual, es válida, en el grafo G2, para ir desde el vértice cuatro hacia el vértice seis es 4, es decir hay que pasar por cuatro lados.
Trayectoria Simple: Es una trayectoria en la que todos los vértices, excepto posiblemente el primero y el último, son diferentes. Por ejemplo, si consideramos el grafo G1, una trayectoria para ir desde el vértice 0 hacia el vértice 3 sería: 0, 2, 1, 3
y esta es una trayectoria simple. Todos los vértices en ella son diferentes.
Si en el mismo grafo G1 consideramos la siguiente trayectoria:
0, 2, 1, 3, 0
también será una trayectoria simple. Todos los vértices son diferentes excepto el primero y el último.
Si consideramos una trayectoria como:
0, 2, 1, 3, 1, 0
esta ya no es una trayectoria simple porque por el vértice 1 se pasa dos veces.
Ciclo: Es una trayectoria simple en la cual el primero y el último vértice son el mismo. Por ejemplo, en el mismo grafo G1 la trayectoria 0, 2, 1, 3, 0 es un ciclo.
Grafo Conectado: Se dice que un grafo es conectado si desde cualquier vértice i del grafo se puede ir hacia cualquier otro vértice j del grafo. Este concepto se usa para grafos no dirigidos. Para grafos dirigidos se utiliza el concepto de grafo fuertemente conectado. Se dice que un grafo dirigido está fuertemente conectado se desde cualquier vértice se puede viajar hacia cualquier otro vértice del grafo.
Para grafos no dirigidos: el máximo número de lados es: \(\frac{n(n – 1)}{2}\) siendo \(n\) el número de vértices del grafo
Para grafos dirigidos: el máximo número de lados es \(n(n – 1)\).
Un grafo dirigido es completo cuando tiene n vértices y \(n(n – 1)\) lados.
Representación de grafos con matrices de adyacencia¶
observa la siguiente implementación y cómo en self.ady_matrix se guarda la información del grafo
import numpy as np
class Graph:
def __init__(self, num_nodes, edge_list, is_directed=False):
assert type(edge_list)==list, "edge_list must be a list of tuples"
assert type(num_nodes)==int, "num_nodes must be an int"
for t in edge_list:
assert len(t)==2, "edge_list must be a list of tuples"
assert t[0]<num_nodes and t[0]>=0 and t[1]<num_nodes and t[1]>=0, "edge number not allowed " + str(t)
self.ady_matrix = np.zeros((num_nodes, num_nodes)).astype(int)
self.is_directed = is_directed
self.num_nodes = num_nodes
for i,j in edge_list:
self.ady_matrix[i,j]=1
if not is_directed:
self.ady_matrix[j,i]=1
g1 = Graph(4, [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)])
g1.ady_matrix
array([[0, 1, 1, 1],
[1, 0, 1, 1],
[1, 1, 0, 1],
[1, 1, 1, 0]])
g2 = Graph(7, [(0,1), (0,2), (1,3), (1,4), (2,5), (2,6)])
g2.ady_matrix
array([[0, 1, 1, 0, 0, 0, 0],
[1, 0, 0, 1, 1, 0, 0],
[1, 0, 0, 0, 0, 1, 1],
[0, 1, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0]])
g3 = Graph(3, [(0,1), (1,0), (1,2), (2,0)], is_directed=True)
g3.ady_matrix
array([[0, 1, 0],
[1, 0, 1],
[1, 0, 0]])
Observa que
para grafos no dirigidos la matriz de adyacencia es simétrica.
la matriz puede ser dispersa, por consiguiente se podrá implementar como una matriz dispersa, como en las notas anteriores.
observa cómo implementamos ciertos métodos
class Graph2(Graph):
def assert_valid_node_number(self, n):
assert n>=0 and n<self.num_nodes, "invalid node number: %d"%n
def grade(self, node_number):
self.assert_valid_node_number(node_number)
return np.sum(self.ady_matrix[node_number]) if not self.is_directed else self.grade_out(node_number)+self.grade_in(node_number)
def grade_out(self, node_number):
assert self.is_directed, "only directed graphs have in/out grades"
self.assert_valid_node_number(node_number)
return np.sum(self.ady_matrix[node_number])
def grade_in(self, node_number):
assert self.is_directed, "only directed graphs have in/out grades"
self.assert_valid_node_number(node_number)
return np.sum(self.ady_matrix[:, node_number])
def are_adyacent(self, node_number_1, node_number_2):
self.assert_valid_node_number(node_number_1)
self.assert_valid_node_number(node_number_2)
return self.ady_matrix[node_number_1, node_number_2]==1 or self.ady_matrix[node_number_2, node_number_1]==1
def is_valid_trayectory(self, trayectory):
assert type(trayectory)==list, "trayectory must be a list"
n = trayectory[0]
self.assert_valid_node_number(n)
for i in trayectory[1:]:
self.assert_valid_node_number(i)
if self.ady_matrix[n,i]!=1:
return False
n=i
return True
def is_simple_trayectory(self, trayectory):
return self.is_valid_trayectory(trayectory) and \
len(np.unique(trayectory[1:-1])) == len(trayectory[1:-1]) and \
np.allclose(np.sort(np.unique(trayectory[1:-1])), np.sort(trayectory[1:-1]))
def is_cycle(self, trayectory):
return self.is_simple_trayectory(trayectory) and trayectory[0]==trayectory[-1]
def is_complete(self):
assert self.is_directed, "only directed graphs can be checked if complete"
return np.allclose(1-np.eye(self.ady_matrix.shape[0]), self.ady_matrix)
g1 = Graph2(4, [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)])
for i in range(g1.num_nodes):
print("node",i, ", grade =", g1.grade(i))
node 0 , grade = 3
node 1 , grade = 3
node 2 , grade = 3
node 3 , grade = 3
g3 = Graph2(4, [(0,1), (1,0), (1,2), (2,0), (2,3)], is_directed=True)
for i in range(g3.num_nodes):
print("node",i, ", grade_in =", g3.grade_in(i),", grade_out =", g3.grade_out(i), ", total grade =", g3.grade(i))
node 0 , grade_in = 2 , grade_out = 1 , total grade = 3
node 1 , grade_in = 1 , grade_out = 2 , total grade = 3
node 2 , grade_in = 1 , grade_out = 2 , total grade = 3
node 3 , grade_in = 1 , grade_out = 0 , total grade = 1
print(g3.are_adyacent(0,1))
print(g3.are_adyacent(3,2))
print(g3.are_adyacent(0,3))
True
True
False
t1 = [ 0, 2, 1, 3]
t2 = [ 0, 2, 1, 2, 3]
t3 = [ 0, 2, 1, 3, 0]
print(" trayectory is_valid is_simple is_cycle")
for t in [t1, t2, t3]:
print("%20s"%str(t), "%10s"%g1.is_valid_trayectory(t),"%10s"%g1.is_simple_trayectory(t), "%10s"%g1.is_cycle(t))
trayectory is_valid is_simple is_cycle
[0, 2, 1, 3] True True False
[0, 2, 1, 2, 3] True False False
[0, 2, 1, 3, 0] True True True
g3.is_complete()
False
g3 = Graph2(4, [(0,1), (1,0), (1,2), (2,1), (2,0), (0,2), (2,3), (3,2), (3,0), (0,3), (1,3), (3,1)], is_directed=True)
g3.is_complete()
True