Representación en memoria
Contents
!wget -nc --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/introalgs.v1/main/content/init.py
import init; init.init(force_download=False);
Representación en memoria¶
Objetivos del módulo¶
Conocer cómo se representan las estructuras de datos en la memoria de la máquina y las decisiones y compromisos que realizan los distintos lenguajes de progamación.
Preguntas básicas¶
¿Cómo se hace corresponder la información de una estructura de datos a memoria de la máquina?
¿Qué decisiones y compromisos adquieren los distintos lenguajes y entornos de programación?
¿Cómo afecta esto al rendimiento de nuestros algoritmos?
¿Qué es una fórmula de direccionamiento?
1. Memoria y datos¶
Python: gestión de la memoria¶
Python realiza una gestión completa de la memoria, como en otros lenguajes (Java, etc.). No hay punteros y ciertas libererías de Python gestionan el uso de la memoria para sus estructuras. Por ejemplo numpy implementa muchas funciones en C y nos las ofrece con la sintaxis limpia de Python. Si usamos numpy podemos al menos ver las direcciones de memoria de los arrays.
Ejecuta el siguiente código y prueba con distintos tipos de datos en dtype: np.int32, np.int64, np.float32, np.float64
import numpy as np
a = np.array([1,2,3], dtype=np.float64)
print("array ", a)
print("tipo de datos ", a.dtype)
print("memory positino a o a[0] ", a.ctypes.data)
print("memory position a[1] ", a[1:].ctypes.data)
print("bytes delta de posiciones", a[1:].ctypes.data - a.ctypes.data)
array [1. 2. 3.]
tipo de datos float64
memory positino a o a[0] 94072038473760
memory position a[1] 94072038473768
bytes delta de posiciones 8
En general, la función id da un identificador único de cualquier objeto de Python, aunque no necesariamente es su posición de memoria (depende de la implementación de tu instalación de Python). Nos sirve para ver si dos variables apuntan al mismo contenido.
a = 2
print(type(a), id(a))
b = a
print(type(b), id(b))
<class 'int'> 94072006972480
<class 'int'> 94072006972480
fíjate como un mismo dato puede tener varias etiquetas
xx = [1,2,3]
print(id(xx), xx)
bb = xx
print(id(bb), bb)
140677573928136 [1, 2, 3]
140677573928136 [1, 2, 3]
del(bb)
print(id(bb), bb)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-20-2ef731d4f814> in <module>
1 del(bb)
----> 2 print(id(bb), bb)
NameError: name 'bb' is not defined
print(id(xx), xx)
140677573928136 [1, 2, 3]
fíjate en la siguiente lógica de Python. Reutiliza las cadenas pequeñas aunque explícitamente no hagamos a=b, pero no las cadenas largas.
a = "hola"
print(type(a), id(a))
b = "hola"
print(type(b), id(b))
<class 'str'> 140677574459264
<class 'str'> 140677574459264
a = "hola como estas"
print(type(a), id(a))
b = "hola como estas"
print(type(b), id(b))
<class 'str'> 140677173882096
<class 'str'> 140677173356528
observa que el concepto de igualdad puede ser definido de dos formas:
el contenido referido por una variable es igual al contenido referido por otra variable: =
dos variables se refieren a la misma posición de memoria: is
a = "hola que tal"
b = "hola que tal"
print(id(a))
print(id(b))
print(a==b, a is b)
140677173357424
140677173354672
True False
a = "hola que tal"
b = a
print(id(a))
print(id(b))
print(a==b, a is b)
140677173358512
140677173358512
True True
observa además la semántica de a+=..., que actualiza la propia memoria sin crear nuevos objetos a=a+...
a = [1,2,3]
print(id(a), a)
a = a + [4]
print(id(a), a)
a += [5]
print(id(a), a)
140677174428168 [1, 2, 3]
140677174428360 [1, 2, 3, 4]
140677174428360 [1, 2, 3, 4, 5]
Python tiene una semántica fija para el paso de parámetros: siempre se pasan las referencias a los objetos.
def f(x):
print(id(x), x)
x = 2
print(id(x), x)
a = 29
print(id(a), a)
f(a)
print(id(a), a)
94072006973344 29
94072006973344 29
94072006972480 2
94072006973344 29
observa cómo el siguiente código se ejecuta en Python Tutor
def f(x):
print(id(x), x)
x.append(32)
print(id(x), x)
a = ["hola", 10, "20"]
print(id(a), a)
f(a)
print(id(a), a)
140677574373960 ['hola', 10, '20']
140677574373960 ['hola', 10, '20']
140677574373960 ['hola', 10, '20', 32]
140677574373960 ['hola', 10, '20', 32]
2. Alineamiento de datos y rendimiento¶
La memoria de un computador es lineal. El lenguaje de programación (compilado o interpretado) es el que la maneja y decide la organización de los datos cuando tenemos estructuras complejas. Es decir, decide cómo linearizar cualquier estructura de datos.
Pero físicamente la manera más eficiente de recorrer la memoria de una máquina también es linealmente, por tanto nuestra aplicación será más o menos eficiente en función de cómo recorra una estructura de datos en relación a cómo se linearizó.
Por tanto, es fundamental entender las decisiones que toma nuestro entorno de programación respecto al almacenaje de estructuras en memoria. Los siguientes experimentos están diseñados para que te familiarices con esto.
Fíjate cómo lineariza numpy una matriz 2D en memoria. Prueba con distintos tipos de datos.
a = np.random.randint(100, size=(3,5)).astype(np.int32)
a
array([[98, 68, 19, 14, 1],
[30, 47, 0, 4, 0],
[71, 52, 75, 28, 9]], dtype=int32)
import itertools
def get_mempositions(a, relative=False):
m = np.zeros(a.shape, dtype=np.int64)
for ii in itertools.product(*[list(range(i)) for i in a.shape]):
m[ii] = a[tuple([slice(i, None, None) for i in ii])].ctypes.data
return m if not relative else m-np.min(m)
print("memory positions of each element of a")
print(get_mempositions(a))
memory positions of each element of a
[[94072037346320 94072037346324 94072037346328 94072037346332
94072037346336]
[94072037346340 94072037346344 94072037346348 94072037346352
94072037346356]
[94072037346360 94072037346364 94072037346368 94072037346372
94072037346376]]
print("memory positions of each element of a, relative to init")
print(get_mempositions(a, relative=True))
memory positions of each element of a, relative to init
[[ 0 4 8 12 16]
[20 24 28 32 36]
[40 44 48 52 56]]
Este es un orden en el que se recorre primero las columnas y luego las filas
la fórmula de direccionamiento en este caso es:
donde
\(k\) es la posición de inicio del array
\(n\_cols\) es en número de columnas del array
\(size\) es el tamaño en bytes del tipo de dato que almacena el array.
\(i,j\) es la \(fila\), \(columna\) de la cual se quiere obtener la posición en memoria
y lo comprobamos
m = np.zeros(a.shape, dtype=int)
size = a.dtype.itemsize
for i in range(a.shape[0]):
for j in range(a.shape[1]):
m[i,j] = (i*a.shape[1] + j)*size
m
array([[ 0, 4, 8, 12, 16],
[20, 24, 28, 32, 36],
[40, 44, 48, 52, 56]])
con numpy también podemos especificar que queremos el orden inverso. Es decir, recorriendo primero las filas y luego las columnas. Esto es típico de FORTRAN. En cambio en C el orden es por filas como anteriormente.
a = np.random.randint(100, size=(3,5)).astype(np.int32)
a = np.asfortranarray(a)
print(get_mempositions(a, relative=True))
[[ 0 12 24 36 48]
[ 4 16 28 40 52]
[ 8 20 32 44 56]]
la fórmula de direccionamiento en este caso es:
y lo comprobamos
m = np.zeros(a.shape, dtype=int)
size = a.dtype.itemsize
for i in range(a.shape[0]):
for j in range(a.shape[1]):
m[i,j] = (i + j*a.shape[0])*size
m
array([[ 0, 12, 24, 36, 48],
[ 4, 16, 28, 40, 52],
[ 8, 20, 32, 44, 56]])
fíjate ahora en el siguiente experimento, en el que recorremos las columnas para sumar
a.sum(axis=1)
array([298, 341, 421])
o recorremos las filas
a.sum(axis=0)
array([222, 232, 218, 151, 237])
y medimos el tiempo en realizar cada operación. Observa que realizamos los experimentos con una matriz cuadrada \((n,n)\) con lo que el número de operaciones en todos los casos es el mismo.
Con el almacenamiento recorriendo por columnas
import matplotlib.pyplot as plt
%matplotlib inline
dtype = np.int32
trows, tcols = [], []
n_set = [100,500,1000,1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000]
for n in n_set:
print (n, end=" ")
k = np.zeros ((n,n)).astype(dtype)
t = %timeit -o -q -r 3 -n 3 k.sum(axis=0)
trows.append(t.best)
t = %timeit -o -q -r 3 -n 3 k.sum(axis=1)
tcols.append(t.best)
plt.plot(n_set, trows, label="rows")
plt.plot(n_set, tcols, label="cols")
plt.xlabel("size of array")
plt.ylabel("time")
plt.grid()
plt.legend()
100 500 1000 1500 2000 2500 3000 3500 4000 4500 5000
<matplotlib.legend.Legend at 0x7ff216c69e48>
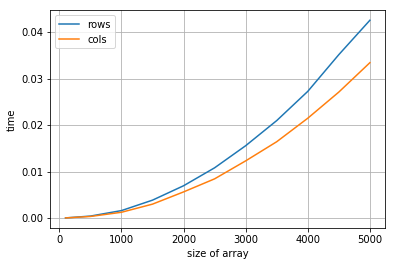
Con el almacenamiento recorriendo por filas
dtype = np.int32
trows, tcols = [], []
n_set = [100,500,1000,1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000]
for n in n_set:
print (n, end=" ")
k = np.zeros ((n,n)).astype(dtype)
k = np.asfortranarray(k)
t = %timeit -o -q -r 3 -n 3 k.sum(axis=0)
trows.append(t.best)
t = %timeit -o -q -r 3 -n 3 k.sum(axis=1)
tcols.append(t.best)
plt.plot(n_set, trows, label="rows")
plt.plot(n_set, tcols, label="cols")
plt.xlabel("size of array")
plt.ylabel("time")
plt.grid()
plt.legend()
100 500 1000 1500 2000 2500 3000 3500 4000 4500 5000
<matplotlib.legend.Legend at 0x7ff216ba6d68>
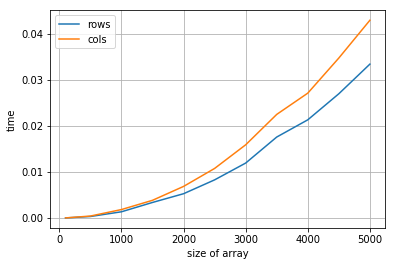
Especificación del orden de almacenamiento¶
Cuando el almacenamiento en memoria de un array es con la con convención de C, se recorren primero las columnas (eje 1) y luego las filas (eje 0). En este caso se describe con la tupla (1,0), indicando qué eje se recorre primero para almacenar en memoria.
a = np.random.randint(100, size=(2,2)).astype(np.int32)
print(get_mempositions(a, relative=True))
[[ 0 4]
[ 8 12]]
fíjate cómo al recorrer el eje 1 se llena una matriz
a = np.zeros((4,5)).astype(int)
for i in range(a.shape[1]):
a[0,i] = i
print(a)
[[0 1 2 3 4]
[0 0 0 0 0]
[0 0 0 0 0]
[0 0 0 0 0]]
en cambio cuando se usa la convención de FORTRAN para almacenar en memoria, el orden es al reves y se describe con la tupla (0,1)
a = np.random.randint(100, size=(2,2)).astype(np.int32)
a = np.asfortranarray(a)
print(get_mempositions(a, relative=True))
[[ 0 8]
[ 4 12]]
fíjate en este caso cómo sucede al recorrer por el eje 0
a = np.zeros((4,5)).astype(int)
for i in range(a.shape[0]):
a[i,0] = i
print(a)
[[0 0 0 0 0]
[1 0 0 0 0]
[2 0 0 0 0]
[3 0 0 0 0]]
fíjate en el caso de \(n=3\) con matrices de tres dimensiones. Con la convención de C, el orden de ejes es (2,1,0)
a = np.random.randint(100, size=(2,3,4)).astype(np.int32)
print(get_mempositions(a, relative=True))
[[[ 0 4 8 12]
[16 20 24 28]
[32 36 40 44]]
[[48 52 56 60]
[64 68 72 76]
[80 84 88 92]]]
En este caso no es obvio identificar cada eje. Usa el siguiente código para visualizar cual es cada eje
print("eje 0")
a = np.zeros((2,3,4)).astype(int)
for i in range(a.shape[0]):
a[i,0,0] = i
print(a)
print("\neje 1")
a = np.zeros((2,3,4)).astype(int)
for i in range(a.shape[1]):
a[0,i,0] = i
print(a)
print("\neje 2")
a = np.zeros((2,3,4)).astype(int)
for i in range(a.shape[2]):
a[0,0,i] = i
print(a)
eje 0
[[[0 0 0 0]
[0 0 0 0]
[0 0 0 0]]
[[1 0 0 0]
[0 0 0 0]
[0 0 0 0]]]
eje 1
[[[0 0 0 0]
[1 0 0 0]
[2 0 0 0]]
[[0 0 0 0]
[0 0 0 0]
[0 0 0 0]]]
eje 2
[[[0 1 2 3]
[0 0 0 0]
[0 0 0 0]]
[[0 0 0 0]
[0 0 0 0]
[0 0 0 0]]]
pero con la convención de FORTRAN, el orden es (0,1,2)
a = np.random.randint(100, size=(2,3,4)).astype(np.int32)
a = np.asfortranarray(a)
print(get_mempositions(a, relative=True))
[[[ 0 24 48 72]
[ 8 32 56 80]
[16 40 64 88]]
[[ 4 28 52 76]
[12 36 60 84]
[20 44 68 92]]]
juega igualmente para entender cual es cada eje como en el ejemplo anterior
Slicing en Python¶
Fíjate cómo podemos indexar de manera genérica cualquier estructura de Python a través de objetos slice (ejemplos)
a = np.random.randint(10, size=(3,10))
a
array([[0, 4, 9, 8, 1, 1, 4, 4, 6, 8],
[1, 8, 6, 2, 7, 0, 7, 8, 2, 5],
[5, 5, 6, 1, 7, 0, 5, 8, 4, 6]])
estas dos operaciones son equivalentes
print(a[:, 3:8])
print(a[slice(None, None, None), slice(3,8,None)])
[[8 1 1 4 4]
[2 7 0 7 8]
[1 7 0 5 8]]
[[8 1 1 4 4]
[2 7 0 7 8]
[1 7 0 5 8]]
y podemos construir especificaciones de slices programáticamente y usarlas como cualquier otra variable
slices = tuple([slice(2,5,None) if i==len(a.shape)-1 else slice(None, None, None) for i in range(len(a.shape))])
print(a[slices])
[[9 8 1]
[6 2 7]
[6 1 7]]
fíjate que la expresión anterior funciona si tenemos más dimensiones
a = np.random.randint(10, size=(2,3,8))
print(a)
[[[2 3 2 5 6 4 8 7]
[7 7 8 3 0 3 7 5]
[4 4 0 5 0 5 5 6]]
[[3 7 2 3 9 3 4 4]
[3 9 5 4 5 7 0 2]
[7 2 3 1 2 4 8 9]]]
slices = tuple([slice(2,5,None) if i==len(a.shape)-1 else slice(None, None, None) for i in range(len(a.shape))])
print(a[slices])
[[[2 5 6]
[8 3 0]
[0 5 0]]
[[2 3 9]
[5 4 5]
[3 1 2]]]
Ejercicios propuestos:¶
Determine una fórmula de direccionamiento para representar un arreglo de tres dimensiones en memoria.
Determina una fórmula de direccionamiento para un arreglo de \(n\) dimensiones en memoria.