Simulated annealing
Contents
!wget -nc --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/introalgs.v1/main/content/init.py
import init; init.init(force_download=False);
Simulated annealing¶
Refs:
Original paper: Kirkpatrick, S., Gelatt, C.D., and Vecchi, M.P., “Optimization by Simulated Annealing,” Science, Volume 220, Number 4598, 13 May 1983, pp. 671- 680
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
w_size = 100
n_cities = 20
cities = (np.random.random((n_cities,2))*w_size).astype(int)
cities = np.array([[ 2,88],[87,84],[84,6],[99,37], [60, 87], [ 8, 83], [43, 33], [45, 66], [28, 94], [ 3, 56], [14, 92], [88, 10], [33, 12], [33, 85], [69, 60], [67, 58], [80, 19], [81, 30], [69, 21], [78, 35]])
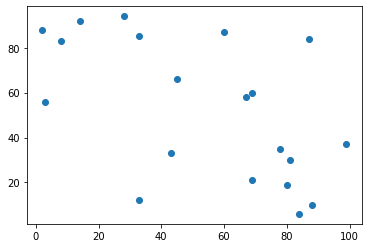
plt.scatter(cities[:,0], cities[:,1])
def TSP_cost(cities, solution):
sol_cities = cities[solution]
return np.sum(np.sqrt(np.sum((sol_cities - np.roll(sol_cities,-1, axis=0))**2, axis=1)))
sol = np.random.permutation(len(cities))
print(sol)
[ 2 6 15 14 12 11 18 9 5 8 0 10 19 16 3 17 4 13 7 1]
Creamos una función que para obtener un vecino de cualquier solución¶
def TSP_neighbour(solution):
i1 = np.random.randint(len(solution))
i2 = i1+1 if i1<len(solution)-1 else 0
r = np.copy(solution)
r[i1]=solution[i2]
r[i2]=solution[i1]
return r
def TSP_neighbour2(solution):
return TSP_neighbour(TSP_neighbour(solution))
Usamos las mismas funciones para el TSP de las notas anteriores¶
def TSP_initialize_population(n_individuals, n_cities):
r = []
for i in range(n_individuals):
r.append(np.random.permutation(n_cities))
return np.array(r)
def TSP_cost(cities, solution):
sol_cities = cities[solution]
return np.sum(np.sqrt(np.sum((sol_cities - np.roll(sol_cities,-1, axis=0))**2, axis=1)))
def TSP_plot_solution(cities, solution):
plt.scatter(cities[:,0], cities[:,1])
plt.plot(cities[solution,0].tolist()+[cities[solution[0],0]], cities[solution,1].tolist()+[cities[solution[0],1]])
plt.scatter(cities[solution[0],0], cities[solution[0],1], marker="x", s=60, c="red", lw="5")
plt.title("cost %.3f"%(TSP_cost(cities, solution)))
def TSP_plot_result(best, bests, means, stds):
fig = plt.figure(figsize=(12,4))
fig.add_subplot(121)
plot_evolution(bests, means, stds)
fig.add_subplot(122)
TSP_plot_solution(cities, best)
Hemos un bucle bajando la temperatura¶
%%writefile sa.py
import numpy as np
import matplotlib.pyplot as plt
import progressbar
pbar = progressbar.progressbar
def plot_evolution(bests, means, stds):
plt.plot(means, label="means")
plt.plot(bests, label="bests")
plt.fill_between(range(len(means)), means-stds, means+stds, color="yellow", alpha=0.2)
plt.legend()
def run_sa(n_individuals, n_cooling_steps, init_population_function, cost_function, generate_neighbor_function):
pop = init_population_function(n_individuals)
mean_costs = []
std_costs = []
best_costs = []
best_sols = []
min_cost = np.inf
min_sol = None
for T in pbar(np.linspace(1,0,n_cooling_steps)):
costs = []
for i in range(len(pop)):
sol = pop[i]
cost_sol = cost_function(sol)
# generate a neighbour
nbr = generate_neighbor_function(sol)
cost_nbr = cost_function(nbr)
# if the neighbour is better
if cost_nbr<cost_sol or np.random.random()<T:
sol = nbr
cost_sol = cost_nbr
pop[i] = sol
costs.append(cost_sol)
if cost_sol < min_cost:
min_sol = np.copy(pop[i])
min_cost = cost_function(pop[i])
best_costs.append(np.min(costs))
mean_costs.append(np.mean(costs))
std_costs.append(np.std(costs))
mean_costs = np.array(mean_costs)
std_costs = np.array(std_costs)
best_costs = np.array(best_costs)
return min_sol, best_costs, mean_costs, std_costs
Writing sa.py
Con pocos individuos y pocos pasos de enfrieamiento¶
%run sa.py
n_individuals = 20
n_cooling_steps = 5000
bestsol, bests, means, stds = run_sa(n_individuals = n_individuals,
n_cooling_steps = n_cooling_steps,
init_population_function = lambda x: TSP_initialize_population(x, n_cities),
cost_function = lambda x: TSP_cost(cities, x),
generate_neighbor_function = TSP_neighbour2)
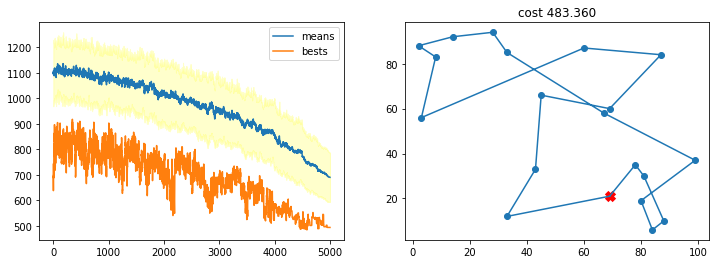
TSP_plot_result(bestsol, bests, means, stds)
100% (5000 of 5000) |####################| Elapsed Time: 0:00:14 Time: 0:00:14
<Figure size 432x288 with 0 Axes>
Con pocos individuos y muchos pasos de enfrieamiento¶
n_individuals = 20
n_cooling_steps = 10000
bestsol, bests, means, stds = run_sa(n_individuals = n_individuals,
n_cooling_steps = n_cooling_steps,
init_population_function = lambda x: TSP_initialize_population(x, n_cities),
cost_function = lambda x: TSP_cost(cities, x),
generate_neighbor_function = TSP_neighbour)
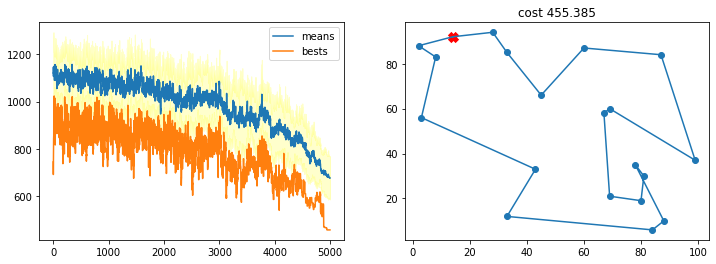
TSP_plot_result(bestsol, bests, means, stds)
ERROR:root:File `'tmp/sa.py'` not found.
100% (10000 of 10000) |##################| Elapsed Time: 0:00:23 Time: 0:00:23
n_individuals = 40
n_cooling_steps = 10000
bestsol, bests, means, stds = run_sa(n_individuals = n_individuals,
n_cooling_steps = n_cooling_steps,
init_population_function = lambda x: TSP_initialize_population(x, n_cities),
cost_function = lambda x: TSP_cost(cities, x),
generate_neighbor_function = TSP_neighbour2)
100% (10000 of 10000) |##################| Elapsed Time: 0:00:51 Time: 0:00:51
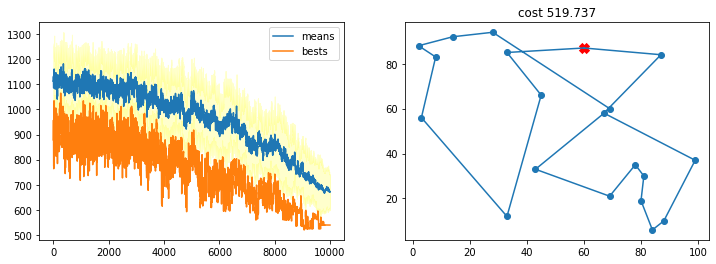
TSP_plot_result(bestsol, bests, means, stds)
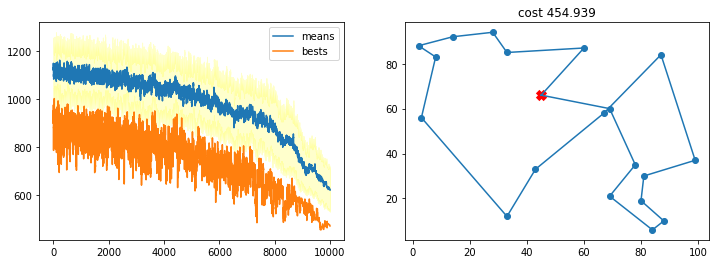
Con muchos individuos y no tantos pasos de enfrieamiento¶
(puede demorar uno o dos minutos)
n_individuals = 100
n_cooling_steps = 5000
bestsol, bests, means, stds = run_sa(n_individuals = n_individuals,
n_cooling_steps = n_cooling_steps,
init_population_function = lambda x: TSP_initialize_population(x, n_cities),
cost_function = lambda x: TSP_cost(cities, x),
generate_neighbor_function = TSP_neighbour)
TSP_plot_result(bestsol, bests, means, stds)
100% (5000 of 5000) |####################| Elapsed Time: 0:00:55 Time: 0:00:55