Algoritmos sobre grafos
Contents
!wget -nc --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/introalgs.v1/main/content/init.py
import init; init.init(force_download=False);
Algoritmos sobre grafos¶
Objetivo del módulo¶
Conocer lo que es un spanning tree y los algoritmos con los cuales se construye spanning tree de costo mínimo en grafos no dirigidos.
Determinar la distancia mínima y el camino más corto para ir desde un vértice hacia los demás en grafos dirigidos.
Preguntas¶
¿Qué es un spanning tree?
¿Para qué se utiliza el algoritmo de Kruskal?
¿Para qué se utiliza el algoritmo de Prim?
¿Para qué se utiliza el algoritmo de Dijkstra?
¿Para qué se utiliza el algoritmo de Floyd?
¿Para qué se utiliza el algoritmo de Warshall?
Generación aleatoria de grafos¶
Observa el código siguiente para entender cómo generamos grafos de manera aleatoria de forma que:
los nodos tienen una posición
los lados tienen un peso
Generando grafos de esta manera podemos experimentar y construir las intuiciones de los algoritmos que estamos tratando.
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
%matplotlib inline
def create_random_graph(directed=False, w_size=200, n_cities=7, prob_connected=0.5):
import itertools
cities = (np.random.random((n_cities,2))*w_size).astype(int)
g = nx.DiGraph() if directed else nx.Graph()
for node_id, location in enumerate(cities):
g.add_node(node_id, pos=location)
for i,j in itertools.product(list(range(len(cities))), list(range(len(cities)))):
if i<j and np.random.random()<prob_connected:
g.add_edge(i,j,weight=np.round(np.linalg.norm(cities[i]-cities[j]),2))
if directed and np.random.random()>.5:
g.add_edge(j,i,weight=np.round(np.linalg.norm(cities[i]-cities[j]),2))
return g
def draw_graph(g,node_size=500, font_color="white",
show_edge_labels=True, edge_units=" km",
x_units="km lon", y_units="km lat"):
positions = {i: g.nodes[i]["pos"] for i in g.nodes} if "pos" in list(g.nodes.values())[0].keys() else None
nx.drawing.draw(g, with_labels=True, pos=positions,
node_alpha=.5, node_color="blue", width=2,
node_size=node_size, font_color=font_color)
if show_edge_labels and positions is not None:
nx.draw_networkx_edge_labels(g, pos=positions,
edge_labels={i:"%.1f%s"%(g.get_edge_data(*i)["weight"],edge_units) for i in g.edges});
plt.axis("on")
plt.xlabel(x_units)
plt.ylabel(y_units)
plt.grid()
plt.axis("equal");
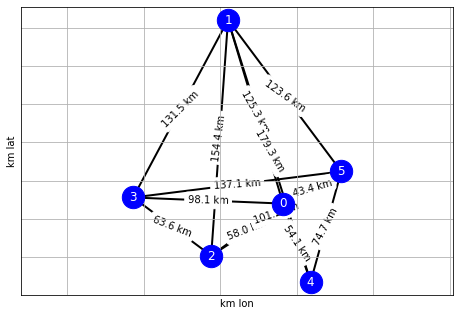
observa cómo con estas funciones creamos y visualizamos un grafo aleatorio. Experimenta con los parámetros para entender qué tipos de grafos puedes generar.
g = create_random_graph(n_cities=6, prob_connected=.9)
draw_graph(g)
Spanning tree¶
DEFINIR SPANNING TREE cableado
Algoritmo de Kruskal para la obtención del spanning tree de costo mínimo (MST)¶
INPUT:
E: lista de lados (edges) del grafo ordenada ascendientemente por costeVset: lista de conjuntos unitarios con los vértices (nodes) del grafo.
PSEUDOCÓDIGO
1. st = {}
2. para cada lado en E
3. si lado (u, w) no forma ciclo en st
4. incluír lado (u, w) en st
5. unir en Vset los subconjuntos que contenga a u y a w
OUTPUT:
st: lista de lados (edges) que conforman el MST
def get_mst(g, illustrate=False):
sorted_edges = [tuple(i) for i in np.r_[[i for i in g.edges]][np.argsort([g.edges[i]["weight"] for i in g.edges])]]
vsets = [set([i]) for i in g.nodes]
# --- begin cosmetics ----
if illustrate:
print("starting vsets", ", ".join(["{"+",".join([str(i) for i in s])+"}" for s in vsets]))
xs = [i["pos"][0] for i in g.nodes.values()]
ys = [i["pos"][1] for i in g.nodes.values()]
xr = np.max(xs) - np.min(xs)
yr = np.max(ys) - np.min(ys)
print(xr, xs)
# --- end cosmetics ----
st = []
for step_nb, edge in enumerate(sorted_edges):
n0,n1 = edge
# check no cycles: both n0 and n1 are NOT in the same set
if sum([n0 in s and n1 in s for s in vsets])>0:
continue
# add edge to spanning tree
st.append(edge)
# makes the union of all sets containing n1 or n0
containing = [i for i in vsets if n0 in i or n1 in i]
containing = containing[0].union(*containing[1:])
not_containing = [i for i in vsets if not n0 in i and not n1 in i]
vsets = [containing] + not_containing
# --- begin cosmetics ----
if illustrate:
plt.figure(figsize=(2,2))
draw_graph(g.edge_subgraph(st), node_size=200, show_edge_labels=False)
str_vsets = ", ".join(["{"+",".join([str(i) for i in s])+"}" for s in vsets])
plt.title("step %d"%step_nb+" edge "+str(edge)+"\nvsets: "+str_vsets)
plt.grid()
plt.axis("tight")
plt.xlim(np.min(xs)-xr*.1, np.max(xs)+xr*.1)
plt.ylim(np.min(ys)-yr*.1, np.max(ys)+yr*.1)
# --- end cosmetics ----
return g.edge_subgraph(st)
xs = [i["pos"][0] for i in g.nodes.values()]
ys = [i["pos"][1] for i in g.nodes.values()]
creamos un grafo que nosotros definimos o generamos uno aleatorio
g = nx.Graph()
g.add_node(1, pos=(0,10))
g.add_node(2, pos=(0,0))
g.add_node(3, pos=(10,10))
g.add_node(4, pos=(10,0))
g.add_node(5, pos=(15,5))
g.add_edge(1,2, weight=1)
g.add_edge(1,3, weight=4)
g.add_edge(1,4, weight=3)
g.add_edge(2,3, weight=6)
g.add_edge(2,4, weight=2)
g.add_edge(3,4, weight=5)
g.add_edge(3,5, weight=7)
g.add_edge(4,5, weight=8)
## DESCOMENTA LA SIGUIENTE LINEA SI QUIERES USAR UN GRAFO ALEATORIO
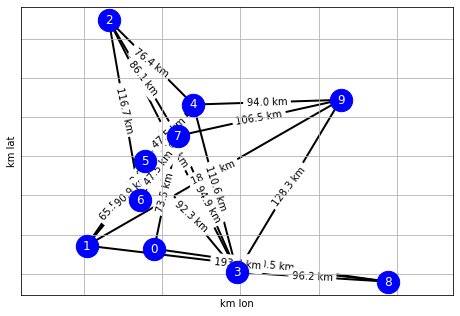
g = create_random_graph(n_cities=10, prob_connected=.6)
draw_graph(g)
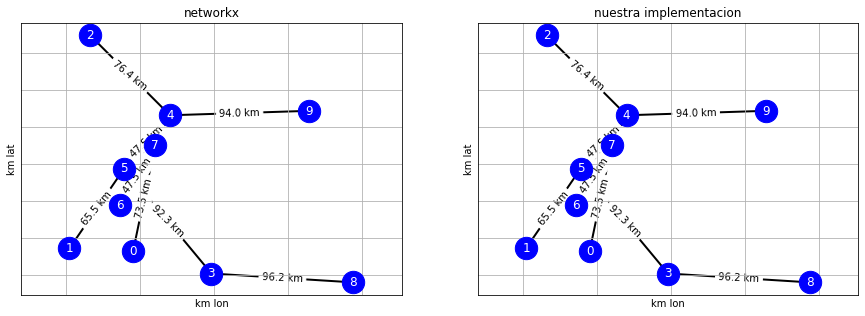
obtenermos el MST (con nuestro algoritmo y con networkx)
n_mst = nx.minimum_spanning_tree(g)
g_mst = get_mst(g)
plt.figure(figsize=(15,5))
plt.subplot(121)
draw_graph(n_mst)
plt.title("networkx")
plt.subplot(122)
draw_graph(g_mst)
plt.title("nuestra implementacion");
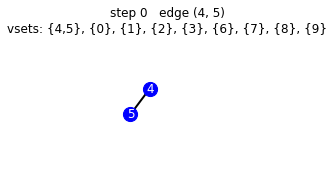
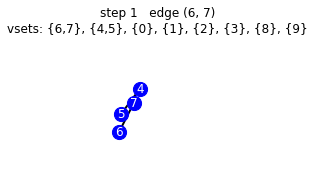
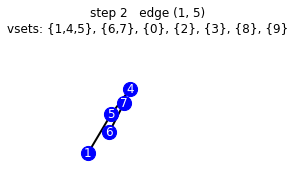
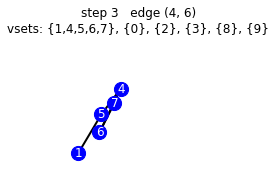
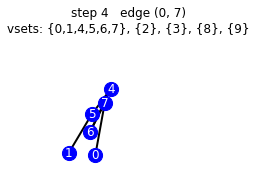
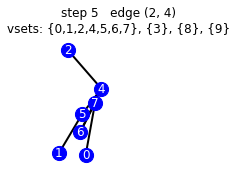
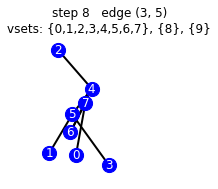
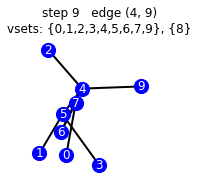
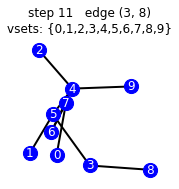
vemos el paso a paso que hace nuestro algoritmo
g_mst = get_mst(g, illustrate=True)
starting vsets {0}, {1}, {2}, {3}, {4}, {5}, {6}, {7}, {8}, {9}
192 [45, 2, 16, 98, 70, 39, 36, 60, 194, 164]
Obtención de distancias y recorridos mínimos¶
g = create_random_graph(n_cities=7, prob_connected=.2, directed=True)
draw_graph(g)
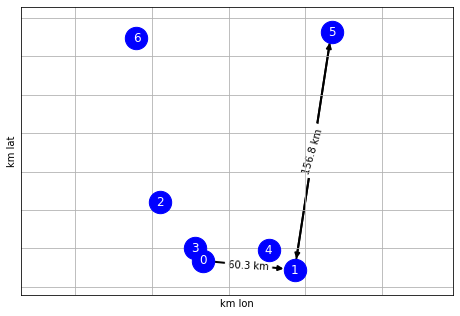
Dijkstra shortest path¶
observa los distintos métodos que tiene network alrededor del Algoritmo de Dijkstra
source, target = 0,1
print("shortest route from",source,"to",target)
print(nx.dijkstra_path(g, source, target))
print("\nshortest route length from",source,"to",target)
print(nx.dijkstra_path_length(g, source, target))
pred, dist = nx.dijkstra_predecessor_and_distance(g, source)
print("\npredecessors to",source)
print(pred)
print("\ndistances to predecessors to", source)
print(dist)
shortest route from 0 to 1
[0, 1]
shortest route length from 0 to 1
60.3
predecessors to 0
{0: [], 1: [0], 5: [1]}
distances to predecessors to 0
{0: 0, 1: 60.3, 5: 217.14999999999998}
dpath = nx.dijkstra_path(g, source, target)
draw_graph(g.subgraph(dpath))
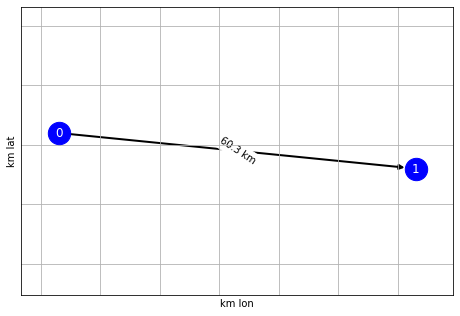
intuición del algoritmo de Dijsktra¶
consideremos el siguiente grafo
g = nx.DiGraph()
g.add_node("S", pos=(0,5))
g.add_node("A", pos=(10,10))
g.add_node("B", pos=(10,0))
g.add_node("C", pos=(20,15))
g.add_node("D", pos=(20,5))
g.add_edge("S","A", weight=5)
g.add_edge("S","B", weight=10)
g.add_edge("A","B", weight=3)
g.add_edge("A","C", weight=7)
g.add_edge("A","D", weight=10)
g.add_edge("B","D", weight=1)
plt.figure(figsize=(3,3))
draw_graph(g, edge_units="")
plt.axis("off");
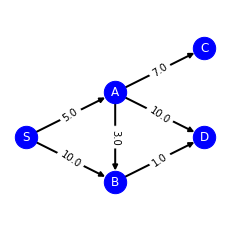
queremos obtener la distancia más corta para ir desde el nodo S al D
Examinamos todos los lados que parten del nodo S
Inferimos que la distancia más corta para llegar al nodo A desde el nodo S es de 5 ya que:
el nodo S solo tiene dos salidas (a través del nodo A y a través del nodo B)
si saliéramos a través del nodo B para llegar al A, empezaríamos con un coste de 10
pero el camino S \(\rightarrow\) A tiene un coste de 5km
esto garantiza que el camino más corto entre S y A es de 5km
Todavía no podemos saber cual es la distancia más corta para llegar a D ya que a D se puede llegar también por B y no sabemos la distancia más corta para llegar a B.
Inferimos que la distancia más corta para llegar a B es de 8 ya que:
al nodo B sólo se puede llegar desde A o S.
ya sabemos cual es la distancia más corta por la que se puede llegar a A o S
Pasando por A, el camino hasta B desde S es de 8km
Directamente desde S, el camino es de 10km
ahora ya podemos inferir que la distancia más corta para llegar a D es de 9km ya que:
sabemos que la distancia más corta para llegar a A es de 5km, y desde ahí hasta D tenemos 10km más.
sabemos que la distancia más corta para llegar a B es de 8km, y desde ahí hasta D tenemos 1km más.
no hay más formas de llegar a D
## Algoritmo de Floyd Warshall
El Algoritmo de Floyd Warshall genera las distancias más cortas entre todos los pares de nodos. Observa las distintas versiones del mismo que proporciona networkx
k = nx.floyd_warshall_numpy(g)
print(k)
[[ 0. 5. 8. 12. 9.]
[inf 0. 3. 7. 4.]
[inf inf 0. inf 1.]
[inf inf inf 0. inf]
[inf inf inf inf 0.]]
k = nx.floyd_warshall(g)
k
{'A': defaultdict(<function networkx.algorithms.shortest_paths.dense.floyd_warshall_predecessor_and_distance.<locals>.<lambda>.<locals>.<lambda>>,
{'A': 0, 'B': 3, 'C': 7, 'D': 4, 'S': inf}),
'B': defaultdict(<function networkx.algorithms.shortest_paths.dense.floyd_warshall_predecessor_and_distance.<locals>.<lambda>.<locals>.<lambda>>,
{'A': inf, 'B': 0, 'C': inf, 'D': 1, 'S': inf}),
'C': defaultdict(<function networkx.algorithms.shortest_paths.dense.floyd_warshall_predecessor_and_distance.<locals>.<lambda>.<locals>.<lambda>>,
{'A': inf, 'B': inf, 'C': 0, 'D': inf, 'S': inf}),
'D': defaultdict(<function networkx.algorithms.shortest_paths.dense.floyd_warshall_predecessor_and_distance.<locals>.<lambda>.<locals>.<lambda>>,
{'A': inf, 'B': inf, 'C': inf, 'D': 0, 'S': inf}),
'S': defaultdict(<function networkx.algorithms.shortest_paths.dense.floyd_warshall_predecessor_and_distance.<locals>.<lambda>.<locals>.<lambda>>,
{'A': 5, 'B': 8, 'C': 12, 'D': 9, 'S': 0})}
preds, distances = nx.floyd_warshall_predecessor_and_distance(g)
print("\npredecessors")
print(preds)
print("\ndistances")
print(distances)
predecessors
{'S': {'A': 'S', 'B': 'A', 'C': 'A', 'D': 'B'}, 'A': {'B': 'A', 'C': 'A', 'D': 'B'}, 'B': {'D': 'B'}}
distances
{'S': defaultdict(<function floyd_warshall_predecessor_and_distance.<locals>.<lambda>.<locals>.<lambda> at 0x7ff0f1b8cd90>, {'S': 0, 'A': 5, 'B': 8, 'C': 12, 'D': 9}), 'A': defaultdict(<function floyd_warshall_predecessor_and_distance.<locals>.<lambda>.<locals>.<lambda> at 0x7ff0f1bb2620>, {'A': 0, 'B': 3, 'C': 7, 'D': 4, 'S': inf}), 'B': defaultdict(<function floyd_warshall_predecessor_and_distance.<locals>.<lambda>.<locals>.<lambda> at 0x7ff0f1bb2158>, {'B': 0, 'D': 1, 'S': inf, 'A': inf, 'C': inf}), 'C': defaultdict(<function floyd_warshall_predecessor_and_distance.<locals>.<lambda>.<locals>.<lambda> at 0x7ff0f1bb22f0>, {'C': 0, 'S': inf, 'A': inf, 'B': inf, 'D': inf}), 'D': defaultdict(<function floyd_warshall_predecessor_and_distance.<locals>.<lambda>.<locals>.<lambda> at 0x7ff0f1bb2378>, {'D': 0, 'S': inf, 'A': inf, 'B': inf, 'C': inf})}