Árboles de búsqueda
Contents
!wget -nc --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/introalgs.v1/main/content/init.py
import init; init.init(force_download=False);
Árboles de búsqueda¶
Objetivo del módulo¶
Conocer el uso de la estructura de árboles binarios para la ordenación de datos
Preguntas¶
¿Cómo se puede mantener ordenado un árbol binario?
¿Qué ventajas tendría mantenerlo ordenado?
¿Qué resultados dan los distintos tipos de recorridos sobre el árbol?
¿Cómo podemos mantener un árbol binario balanceado?
Observa la siguiente implementación¶
usamos explícitamente estructuras para almacenar un hijoz izquierdo y uno derecho
tenemos un algoritmo para insertar elementos garantizando un cierto orden
los recorridos sobre dicho orden nos producen listas ordenadas
la complejidad computacional de cada operación
import numpy as np
class BTNode:
def __init__(self, value, left=None, right=None):
self.value = value
self.left = None
self.right = None
if left is not None:
self.add_left(left)
if right is not None:
self.add_right(right)
def add_left(self, value):
assert self.left is None, "node already has left child"
self.left = self.__class__(value) if not isinstance(value,self.__class__) else value
return self
def add_right(self, value):
assert self.right is None, "node already has right child"
self.right = self.__class__(value) if not isinstance(value,self.__class__) else value
return self
def swap_children(self):
tmp = self.left
self.left = self.right
self.right = self.left
return self
def insert_ordered(self, new_value):
if new_value < self.value:
if self.left is None:
self.add_left(new_value)
else:
self.left.insert_ordered(new_value)
else:
if self.right is None:
self.add_right(new_value)
else:
self.right.insert_ordered(new_value)
return self
def ird(self):
if self.value==None:
return []
s1 = self.left.ird() if self.left is not None else []
s2 = self.right.ird() if self.right is not None else []
return s1+[self.value]+s2
def to_indented_string(self, level, prefix=""):
s = (" "*2*level + prefix + str(self.value) + "\n") if self.value is not None else ""
s += self.left.to_indented_string(level+1, prefix="L: ") if self.left is not None else ""
s += self.right.to_indented_string(level+1, prefix="R: ") if self.right is not None else ""
return s
def __repr__(self):
return self.to_indented_string(0)
@classmethod
def from_list(cls, a_list):
r = cls(a_list[0])
for i in a_list[1:]:
r.insert_ordered(i)
return r
@classmethod
def sort_list(cls, a_list):
r = cls.from_list(a_list)
return np.r_[r.ird()]
### podemos crear un árbol con un orden arbitrario
k=BTNode(10)\
.add_right(BTNode(20)\
.add_left(BTNode(15)\
.add_left(91))\
.add_right(21))\
.add_left(12)
k
10
L: 12
R: 20
L: 15
L: 91
R: 21
k.ird()
[12, 10, 91, 15, 20, 21]
podemos crear un árbol manteniendo la siguiente propiedad:¶
para cualquier nodo, su hijo izquierdo es menor y su hizo derecho es mayor
k = BTNode(10).insert_ordered(2).insert_ordered(12).insert_ordered(1).insert_ordered(4)
k
10
L: 2
L: 1
R: 4
R: 12
k = BTNode.from_list([10,2,12,1,4])
k
10
L: 2
L: 1
R: 4
R: 12
de modo que al recorrerlo nos produce una lista ordenada
k.ird()
[1, 2, 4, 10, 12]
BTNode.sort_list([10,43,12,1,-20])
array([-20, 1, 10, 12, 43])
np.random.permutation(100)[:10]
array([23, 47, 42, 12, 28, 70, 84, 2, 92, 6])
for _ in range(10):
l = np.random.permutation(100)[:10]
print(l,"-->", end=' ')
print(BTNode.sort_list(l))
[65 40 34 58 53 17 52 27 45 31] --> [17 27 31 34 40 45 52 53 58 65]
[ 5 91 60 3 4 92 17 38 74 2] --> [ 2 3 4 5 17 38 60 74 91 92]
[81 98 11 64 73 25 32 77 20 55] --> [11 20 25 32 55 64 73 77 81 98]
[13 65 4 78 60 98 10 29 27 43] --> [ 4 10 13 27 29 43 60 65 78 98]
[72 16 40 78 8 88 0 49 18 86] --> [ 0 8 16 18 40 49 72 78 86 88]
[67 38 74 91 48 8 9 39 34 7] --> [ 7 8 9 34 38 39 48 67 74 91]
[53 14 35 33 32 58 8 95 24 49] --> [ 8 14 24 32 33 35 49 53 58 95]
[77 12 22 68 72 2 33 58 35 37] --> [ 2 12 22 33 35 37 58 68 72 77]
[16 71 29 19 57 76 85 95 27 6] --> [ 6 16 19 27 29 57 71 76 85 95]
[67 90 99 21 81 33 94 39 8 76] --> [ 8 21 33 39 67 76 81 90 94 99]
observa que, en la lección anterior, ordenábamos in situ y ahora creamos una estructura nueva.
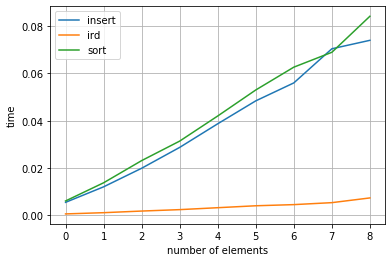
finalmente, medimos rendimiento
def experiment_insert_ordered(n):
k = np.random.permutation(100*n)[:n]
tree = BTNode(k[0])
for i in k:
tree.insert_ordered(i)
return tree
def experiment_sort(n):
k = np.random.permutation(100*n)[:n]
BTNode.sort_list(k)
r_times_insert = []
r_times_ird = []
r_times_sort = []
n_list = np.arange(10,100,10)*100
print("running experiments")
for n in n_list:
print (".", end=" ")
t = %timeit -r 3 -n 3 -o -q experiment_insert_ordered(n)
r_times_insert.append(t.best)
k = experiment_insert_ordered(n)
t = %timeit -r 3 -n 3 -o -q k.ird()
r_times_ird.append(t.best)
t = %timeit -r 3 -n 3 -o -q experiment_sort(n)
r_times_sort.append(t.best)
running experiments
. . . . . . . . .
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(r_times_insert, label="insert")
plt.plot(r_times_ird, label="ird")
plt.plot(r_times_sort, label="sort")
plt.ylabel("time")
plt.xlabel("number of elements")
plt.grid()
plt.legend()
<matplotlib.legend.Legend at 0x7fbc36569080>