Introducción a Python
Contents
!wget -nc --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/introalgs.v1/main/content/init.py
import init; init.init(force_download=False);
Introducción a Python¶
Asignación automatica de tipos de variables¶
En Python no es necesario declarar explícitamente el tipo de las variables. El intérprete trata de inferir el tipo de las variables según se usan. Igualmente, las operaciones tienen semántica distinta para distintos tipos de datos. Fíjate en el ejemplo siguiente. ¿Por qué el resultado de las dos últimas divisiones no es el mismo?
a = 10
b = 3
c = 3.
d = "hola"
print(type(a), type(b), type(c), type(d))
print("a =",a,"; b =",b, "; c =",c)
print("a/b =", a/b)
print("a/c =", a/c)
print("a/b =", a//b)
print("a/c =", a//c)
<class 'int'> <class 'int'> <class 'float'> <class 'str'>
a = 10 ; b = 3 ; c = 3.0
a/b = 3.3333333333333335
a/c = 3.3333333333333335
a/b = 3
a/c = 3.0
Listas¶
a = [1,2,"hola", 3, 2.03, [9,10,11], "adios"]
print(a)
print(len(a))
[1, 2, 'hola', 3, 2.03, [9, 10, 11], 'adios']
7
print(a[2])
hola
print(a[5])
print(a[5][1])
[9, 10, 11]
10
print(a[-1])
adios
print(a[2:5])
['hola', 3, 2.03]
print(a[:3])
[1, 2, 'hola']
print(a[:-2])
[1, 2, 'hola', 3, 2.03]
b = [78, "casa", 23]
print(a+b)
[1, 2, 'hola', 3, 2.03, [9, 10, 11], 'adios', 78, 'casa', 23]
print(a*2)
[1, 2, 'hola', 3, 2.03, [9, 10, 11], 'adios', 1, 2, 'hola', 3, 2.03, [9, 10, 11], 'adios']
Matrices y vectores¶
Con la librería numpy se trabaja con matrices de forma natural. Fíjate cómo se declaran y cómo descubrimos sus dimensiones.
import numpy as np
a = np.array([[1,2,3,4,5],
[5,4,3,2,1],
[9,8,7,6,5],
[7,6,5,6,7],
[2,2,2,3,3],
[4,3,4,3,4],
[5,1,1,4,1]])
print("a shape", a.shape)
print("a rows", a.shape[0])
print("a cols", a.shape[1])
v = np.array([2,3,4,5,6,7,3,12])
print("v shape", v.shape)
print("v elems", v.shape[0])
a shape (7, 5)
a rows 7
a cols 5
v shape (8,)
v elems 8
len(a.shape)
2
Con la notación de índices accedemos a columas o filas enteras, rangos de columnas o filas, elementos individuales o porciones de una matriz o un vector.
print("una fila " ,a[2])
print("una fila ",a[2,:])
print("una columna ",a[:,2])
print("un elemento ",a[2,2])
print("varias filas \n",a[2:5])
print("varias columnas \n",a[:,1:3])
print("una porcion \n",a[2:5,1:3])
una fila [9 8 7 6 5]
una fila [9 8 7 6 5]
una columna [3 3 7 5 2 4 1]
un elemento 7
varias filas
[[9 8 7 6 5]
[7 6 5 6 7]
[2 2 2 3 3]]
varias columnas
[[2 3]
[4 3]
[8 7]
[6 5]
[2 2]
[3 4]
[1 1]]
una porcion
[[8 7]
[6 5]
[2 2]]
Muchas funciones de la librería numpy operan sobre una matriz completa, o de forma separada por columnas o filas según el valor del argumento axis.
print("suma total", np.sum(a))
print("suma eje 0", np.sum(a, axis=0))
print("suma eje 1", np.sum(a, axis=1))
print("promedio total", np.mean(a))
print("promedio eje 0", np.mean(a, axis=0))
print("promedio eje 1", np.mean(a, axis=1))
suma total 138
suma eje 0 [33 26 25 28 26]
suma eje 1 [15 15 35 31 12 18 12]
promedio total 3.942857142857143
promedio eje 0 [4.71428571 3.71428571 3.57142857 4. 3.71428571]
promedio eje 1 [3. 3. 7. 6.2 2.4 3.6 2.4]
Las matrices en Python pueden tener un número arbitrario de dimensiones y podemos acceder a submatrices en la dirección o dimensión que queramos.
z = np.random.randint(100, size=(3,4))
print(z)
[[16 58 68 82]
[ 9 57 25 4]
[41 41 28 25]]
np.sum(z, axis=1)
array([224, 95, 135])
m = np.random.randint(10, size=(3,3,3))
print("Matrix 3D completa\n", m)
print("---\n", m[0,:,:])
print("---\n", m[1,:,:])
print("---\n", m[:,0,:])
print("---\n", m[:,0,0])
print("---\n", np.mean(m, axis=2))
Matrix 3D completa
[[[8 3 4]
[1 6 4]
[2 3 6]]
[[2 1 3]
[6 1 5]
[0 0 0]]
[[6 1 0]
[6 7 9]
[9 2 0]]]
---
[[8 3 4]
[1 6 4]
[2 3 6]]
---
[[2 1 3]
[6 1 5]
[0 0 0]]
---
[[8 3 4]
[2 1 3]
[6 1 0]]
---
[8 2 6]
---
[[5. 3.66666667 3.66666667]
[2. 4. 0. ]
[2.33333333 7.33333333 3.66666667]]
Generación de matrices y vectores¶
print("matrix identidad\n", np.eye(3))
print("vector de ceros", np.zeros(4))
print("matriz de ceros\n", np.zeros((3,2)))
print("matriz de unos\n", np.ones((2,3)))
print("vector rango", np.arange(10))
print("vector rango", np.arange(5,10))
print("vector espacio lineal", np.linspace(-10,5,7))
print("matriz aleatoria según distribución uniforme [0,1]\n", np.random.random(size=(3,5)))
print("vector aleatorio de enteros entre 0 y 5", np.random.randint(5, size=10))
matrix identidad
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
vector de ceros [0. 0. 0. 0.]
matriz de ceros
[[0. 0.]
[0. 0.]
[0. 0.]]
matriz de unos
[[1. 1. 1.]
[1. 1. 1.]]
vector rango [0 1 2 3 4 5 6 7 8 9]
vector rango [5 6 7 8 9]
vector espacio lineal [-10. -7.5 -5. -2.5 0. 2.5 5. ]
matriz aleatoria según distribución uniforme [0,1]
[[0.27561038 0.60018936 0.10123643 0.21804175 0.05370778]
[0.24593263 0.86958971 0.64622179 0.41606127 0.10039678]
[0.09037743 0.68950826 0.51467489 0.96948585 0.70842397]]
vector aleatorio de enteros entre 0 y 5 [3 1 0 2 4 2 2 0 2 4]
Operaciones vectorizadas¶
v = np.array([10,12,13,15,20])
print(v)
print(v+1)
print(v*2)
print(v.dot(v))
[10 12 13 15 20]
[11 13 14 16 21]
[20 24 26 30 40]
1038
a = np.array([[1,2,3],[4,5,6]])
b = np.array([[6,5,4],[3,2,1]])
c = np.array([[1,2],[4,5]])
print(a)
print(b)
print("--")
print(a.T.dot(a))
print(a*b)
[[1 2 3]
[4 5 6]]
[[6 5 4]
[3 2 1]]
--
[[17 22 27]
[22 29 36]
[27 36 45]]
[[ 6 10 12]
[12 10 6]]
a = np.array([[1,2,3],[4,5,6]])
b = np.array([[6,5,4],[3,2,1]])
print(a)
print(b)
print("--")
print("a+b\n",a+b)
print("a**2\n", a**2)
print("a*b\n",a*b)
print("a x b'\n",a.dot(b.T))
print("a' x b\n",a.T.dot(b))
[[1 2 3]
[4 5 6]]
[[6 5 4]
[3 2 1]]
--
a+b
[[7 7 7]
[7 7 7]]
a**2
[[ 1 4 9]
[16 25 36]]
a*b
[[ 6 10 12]
[12 10 6]]
a x b'
[[28 10]
[73 28]]
a' x b
[[18 13 8]
[27 20 13]
[36 27 18]]
a = np.array([1,8,4,10,-4,5])
print(a)
print(a>4)
i = np.array([False, True, False, True, False, True])
print(i)
a[a>4]
[ 1 8 4 10 -4 5]
[False True False True False True]
[False True False True False True]
array([ 8, 10, 5])
Las operaciones vectorizadas también funcionan con expresiones booleanas. Fíjate cómo se indexa un vector con una expresión booleana para seleccionar un conjunto de elementos.
a = np.array([1,8,4,10,-4,5])
print("posiciones en a >4:", a>4)
print("elementos de a >4:",a[a>4])
posiciones en a >4: [False True False True False True]
elementos de a >4: [ 8 10 5]
Funciones y estructuras¶
Python es un lenguaje indentado, no usa corchetes para delimitar el alcance de las estructuras de programación sino que se fija en los cambios de indentación.
No se declara el tipo de los argumentos de las funciones. La semática de la implementación ha de estar preparada para funcionar con los tipos de datos que quieres.
def funcion_1(a,b):
r = a**2
return r+b
def greatest(a,b):
if a>b:
return a
else:
return b
m1 = np.array([[3,4],[1,1]])
m2 = np.array([[5,6],[0,0]])
print(funcion_1 (10.4,2))
print(funcion_1 (10.4, np.array([2,4])))
print(funcion_1 (m1,m2))
print(greatest(10,2))
110.16000000000001
[110.16 112.16]
[[14 22]
[ 1 1]]
10
Podemos definir valores por defecto para los argumentos de las funciones y llamarlas usando explícitamente el nombre de los argumentos. Además, las funciones pueden devolver varios valores.
def f_power(x, p=2):
return x**p
print(f_power(x=3))
print(f_power(p=4, x=3))
9
81
def f_power(x, p=2):
return x**p, x*p
r = f_power(p=4, x=3)
print(r[1])
r1, r2 = f_power(p=4, x=3)
print(r1)
print(r2)
a,b = 10, np.array([10,4,-3])
print(a)
print(b)
12
81
12
10
[10 4 -3]
def f_power(x, p=2):
return x**p
def f_powers(x, p1=2, p2=3):
return x**p1, x**p2
print(f_power(4))
print(f_power(4,3))
print(f_powers(4, p1=3))
xp1, xp2 = f_powers(4, p2=4, p1=3)
print("power1",xp1, "power2", xp2)
16
64
(64, 64)
power1 64 power2 256
m = [3,10,"hola", -23]
for i in m:
print("el elemento es ", i)
el elemento es 3
el elemento es 10
el elemento es hola
el elemento es -23
#range(len(b))
print(b)
print(len(b))
for i in range(len(b)):
print("indice", i, "tiene el valor", b[i])
[10 4 -3]
3
indice 0 tiene el valor 10
indice 1 tiene el valor 4
indice 2 tiene el valor -3
Diccionarios¶
d = {"i1": 16, "nombre": "haskel", "edad": 32}
r10 = list(range(10))
rr = np.random.randint(10, size=10)
print(r10)
print(rr)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[9 8 6 9 7 8 9 2 4 7]
for i in list(d.keys()):
print("la clave", i, "tiene el valor", d[i])
la clave i1 tiene el valor 16
la clave nombre tiene el valor haskel
la clave edad tiene el valor 32
for i in range(len(rr)):
print("el indice", i, "tiene el valor", rr[i])
el indice 0 tiene el valor 9
el indice 1 tiene el valor 8
el indice 2 tiene el valor 6
el indice 3 tiene el valor 9
el indice 4 tiene el valor 7
el indice 5 tiene el valor 8
el indice 6 tiene el valor 9
el indice 7 tiene el valor 2
el indice 8 tiene el valor 4
el indice 9 tiene el valor 7
Los diccionarios son listas de asociaciones entre objetos (como hashes en Java)
d = {"i1": 16, "nombre": "haskel", "edad": 32}
print(d)
print(list(d.keys()))
print(d["nombre"], d["edad"])
for k in list(d.keys()):
print(d[k])
{'i1': 16, 'nombre': 'haskel', 'edad': 32}
['i1', 'nombre', 'edad']
haskel 32
16
haskel
32
Expresiones compactas¶
Fíjate cómo las siguientes expresiones son equivalentes:
a=15
if a > 10:
s = "mayor que 10"
else:
s = "menor que 10"
print(s)
mayor que 10
a = 5
s = "mayor que 10" if a > 10 else "menor que 10"
print(s)
menor que 10
a = [10, -4, 20, 5]
o = ["10A", "-4B", "20A", "5A"]
o = []
for i in a:
if i<0:
o.append(str(i)+"B")
else:
o.append(str(i)+"A")
print(o)
['10A', '-4B', '20A', '5A']
def convert(x):
return str(x)+"B" if x<0 else str(x)+"A"
o = [convert(i) for i in a]
print(o)
['10A', '-4B', '20A', '5A']
r = []
for i in range(10):
r.append("el numero "+str(i))
print(r)
['el numero 0', 'el numero 1', 'el numero 2', 'el numero 3', 'el numero 4', 'el numero 5', 'el numero 6', 'el numero 7', 'el numero 8', 'el numero 9']
r = ["el numero "+str(i) for i in range(10)]
print(r)
['el numero 0', 'el numero 1', 'el numero 2', 'el numero 3', 'el numero 4', 'el numero 5', 'el numero 6', 'el numero 7', 'el numero 8', 'el numero 9']
Gráficos¶
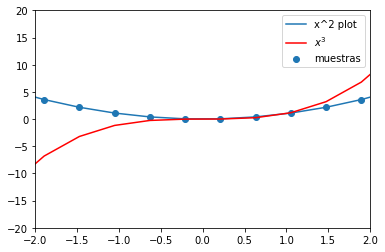
Con plt.plot pintamos puntos conectados, con **plt.scatter” pintamos puntos sueltos
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
x = np.linspace(-4,4,20)
plt.plot(x, x**2, label="x^2 plot")
plt.scatter(x, x**2, label="muestras")
plt.plot(x, x**3, label="$x^3$", color="red")
plt.xlim([-2,2])
plt.ylim([-20, 20])
plt.legend()
<matplotlib.legend.Legend at 0x7f629b3d8eb8>
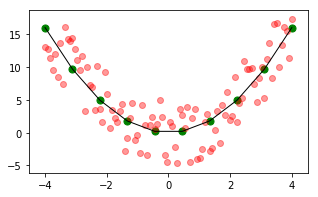
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
plt.figure(figsize=(5,3))
x = np.linspace(-4,4,10)
plt.plot(x, x**2, color="black", linewidth=1)
plt.scatter(x, x**2, c="green", s=50)
x_r = np.linspace(-4,4,100)
x_ruido = x_r**2 + (np.random.random(x_r.shape)-0.5)*10
plt.scatter(x_r,x_ruido, c="red", alpha=0.4)
<matplotlib.collections.PathCollection at 0x7f6274eb80f0>