Listas generalizadas
Contents
!wget -nc --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/introalgs.v1/main/content/init.py
import init; init.init(force_download=False);
Listas generalizadas¶
Objetivos del módulo¶
Entender el concepto de lista generalizada, sus posibles representaciones, su manipulación y su uso
Preguntas básicas¶
¿Qué es una lista generalizada?
¿Cómo se define y se implementa?
¿Qué consecuencias tienen las decisiones de implementación sobre complejidad en las operaciones de la lista?
Introducción¶
Una lista generalizada es un conjunto finito de \(n\) elementos (\(n\ge 0\)) cada uno de los cuales es un átomo u otra lista generalizada. La lista generalizada es una estructura recursiva por definición ya que se define en términos de si mismo. Por ejemplo:
W = (a, (b, c), d, (e, (f, g)), h)
Los átomos se presentan separados por comas, y cuando un elemento sea otra lista, ésta irá entre paréntesis.
Una lista generalizada se puede representar como una lista ligada. La configuración de cada nodo usa 3 campos:
Marca:
0si el nodo es un átomo o1si es una sublistaDato: el átomo o una referencia a una sublista.
Siguiente: Referencia al siguiente nodo o
Nonesi no hay más nodos.
Por ejemplo, la lista anterior se representaría de la siguiente manera.
from IPython.display import Image
Image(filename='local/imgs/lista_generalizada.jpg', width=700)
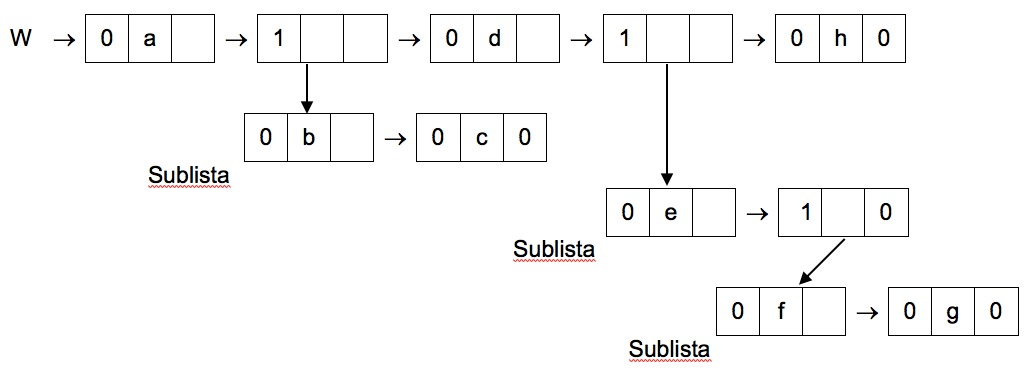
Esta lista se representaría en Python de la siguiente manera
a,b,c,d,e,f,g,h = list(range(8))
W = [a, [b,c], d, [e, [f,g]], h]
print(W)
print(len(W))
print(W[3], ":", W[3][0], ":", W[3][1][0])
[0, [1, 2], 3, [4, [5, 6]], 7]
5
[4, [5, 6]] : 4 : 5
Realicemos nosotros nuestra propia implementación. Para ello definimos una clase para representar cualquier nodo. Observa que no usamos un campo explícito para diferenciar si tenemos un átomo o una nueva lista. Esto lo resolveremos llamando a type.
class Node:
def __init__(self, value, next=None):
assert next is None or isinstance(next,Node), "next must be Node, not %s"%(type(next))
self.value = value
self.next = next
def __repr__(self):
return str(self.value)
n = Node(10, Node(20, Node(30)))
k=n
print(k, end=' ')
while (k.next is not None):
print("--> %s"%k.next, end=' ')
k = k.next
10 --> 20 --> 30
Y definimos una clase para una lista generalizada. Fíjate que no usamos ninguna list de python ya que precisamente es lo que estamos implementando.
class L(object):
def __init__ (self, first_node=None):
assert first_node is None or isinstance(first_node,Node), "first must be Node, not %s"%(type(first_node))
self.first_node = first_node
def __getitem__(self, idx):
k = self.first_node
for i in range(idx):
assert k.next is not None, "index %s out of range"%(str(idx))
k = k.next
return k.value
def __len__(self):
k = self.first_node
if k is None:
return 0
i=1
while k.next is not None:
i+=1
k = k.next
return i
def __repr__ (self):
if self.first_node is None:
return "[]"
s = "[ %s"%self.first_node
k=self.first_node
while (k.next is not None):
s += ", %s"%k.next
k = k.next
return s+" ]"
Fíjate cómo creamos una lista sólo con átomos
W = L(Node(10, Node(20, Node(30))))
print(W)
print("len =", len(W))
[ 10, 20, 30 ]
len = 3
Y una lista con sublistas
W=L(Node(10, Node(L(Node(14, Node(18))), Node(20, Node(30)))))
print(W)
print("len =", len(W))
[ 10, [ 14, 18 ], 20, 30 ]
len = 4
En este caso una sublista va encapsulada dentro de un nodo
print(Node(L(Node(14, Node(18)))))
print(W[1])
print("len sublista =", len(W[1]))
[ 14, 18 ]
[ 14, 18 ]
len sublista = 2
Observa la implementación del método getitem y cómo de manera natural soporta el indexado de sublistas
W=L(Node(10, Node(L(Node(14, Node(18))), Node(20, Node(30)))))
print("the list: ", W)
print("element at 1: ", W[1])
print("element at 2: ", W[2])
print("element of sublist:", W[1][0])
the list: [ 10, [ 14, 18 ], 20, 30 ]
element at 1: [ 14, 18 ]
element at 2: 20
element of sublist: 14
Por supuesto, también soportamos la lista vacía
W = L()
print(W)
print("len = ", len(W))
[]
len = 0
Añadimos un método suma que me concatene dos listas generalizadas
class L(L):
def __add__(self, M):
# obtiene el ultimo elemento de esta lista
k = self.first_node
# si la lista actual no tiene elementos
if k is None:
self.first_node = M.first_node
return self
# en caso contrario la agregamos al ultimo nodo
while k.next is not None:
k = k.next
k.next = M.first_node
return self
W = L(Node(10, Node(20, Node(30))))
Z = L(Node(3, Node(2)))
print(W)
print(Z)
print(W + Z + L())
[ 10, 20, 30 ]
[ 3, 2 ]
[ 10, 20, 30, 3, 2 ]
pero observa que esta implementación modifica la lista del primer argumento de la adición
W = L(Node(10, Node(20, Node(30))))
Z = L(Node(3, Node(2)))
print("antes de sumar")
print("W", W)
print("Z", Z)
X = W + Z
print("después de sumar")
print("W", W)
print("Z", Z)
print("X", X)
antes de sumar
W [ 10, 20, 30 ]
Z [ 3, 2 ]
después de sumar
W [ 10, 20, 30, 3, 2 ]
Z [ 3, 2 ]
X [ 10, 20, 30, 3, 2 ]
esto induce una recursividad infinita cuando hacemos algo como esto:
X = W + Z + W
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
<ipython-input-16-e59663523402> in <module>()
----> 1 X = W + Z + W
<ipython-input-13-1923da9137ce> in __add__(self, M)
12 # en caso contrario la agregamos al ultimo nodo
13 while k.next is not None:
---> 14 k = k.next
15
16 k.next = M.first_node
KeyboardInterrupt:
en los ejercicios reparás este problema
polinomios¶
usemos listas para representar el siguiente polinomio
primero definimos una clase para los términos y luego una subclase de L para representar los polinomios
from IPython.display import Math
class Term(object):
pass
class XYZTerm(Term):
def __init__(self, coef, ex, ey, ez):
assert (isinstance(coef, float) or isinstance(coef,int)) and \
isinstance(ex, int) and \
isinstance(ey, int) and \
isinstance(ez, int) , "coef/exp must be float/int"
self.coef = coef
self.ex = ex
self.ey = ey
self.ez = ez
def get_math_representation(self):
s = "" if self.coef==0 else \
("%s"%str(self.coef) if self.coef!=1 else "") +\
(" x" if self.ex==1 else (" x^%d"%self.ex if self.ex!=0 else "")) +\
(" y" if self.ey==1 else (" y^%d"%self.ey if self.ey!=0 else "")) +\
(" z" if self.ez==1 else (" z^%d"%self.ez if self.ez!=0 else ""))
return s
def show(self):
from IPython.display import Math, HTML, display
display(HTML("<script src='https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.3/latest.js?config=default'></script>"))
return Math(self.get_math_representation())
def __repr__(self):
return self.get_math_representation()
t = XYZTerm(2,4,1,0)
t
2 x^4 y
t.show()
t = XYZTerm(1,4,1,0)
t
x^4 y
class Pol(L):
def get_math_representation(self):
if self.first_node is None:
return Math("")
k = self.first_node
s = k.value.get_math_representation()
while (k.next is not None):
s += "+"+k.next.value.get_math_representation()
k = k.next
s = s.replace("+-", "-")
return s
def show(self):
from IPython.display import Math, HTML, display
display(HTML("<script src='https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.3/latest.js?config=default'></script>"))
return Math(self.get_math_representation())
pol = Pol(Node(XYZTerm(2,3,2,2), Node(XYZTerm(5,3,1,2), Node(XYZTerm(7,1,2,2), \
Node(XYZTerm(5,2,1,1), Node(XYZTerm(4,1,0,1), Node(XYZTerm(4,3,2,0),\
Node(XYZTerm(8,0,1,0), Node(XYZTerm(9,0,0,0) )) ) ) ) ))))
pol
[ 2 x^3 y^2 z^2, 5 x^3 y z^2, 7 x y^2 z^2, 5 x^2 y z, 4 x z, 4 x^3 y^2, 8 y, 9 ]
pol.show()
Pero esta implementación está muy atada a esta forma concreta de polinomios con tres variables, llamadas \(x\), \(y\), \(z\). Creemos una representación más flexible, observando que en el polinomio anterior podemos sacar términos comunes por cada variable.
class VarTerm(Term):
def __init__(self, coef, var, exp=1):
assert (isinstance(coef, float) or isinstance(coef,int)) and \
isinstance(exp, int) and isinstance(var, str) and len(var)==1
self.coef = coef
self.var = var
self.exp = exp
def get_math_representation(self):
s = "" if self.coef==0 else \
("%s"%str(self.coef) if self.coef!=1 else "") +\
(" %s"%self.var if self.exp==1 else (" %s^%d"%(self.var, self.exp) if self.exp!=0 else ""))
return s
def show(self):
from IPython.display import Math, HTML, display
display(HTML("<script src='https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.3/latest.js?config=default'></script>"))
return Math(self.get_math_representation())
def __repr__(self):
return self.get_math_representation()
class VarPol(Pol):
def __init__(self, first_node, vterm=VarTerm(1,"k",0)):
super(VarPol, self).__init__(first_node)
assert vterm is not None and isinstance(vterm, VarTerm), "must specify a VarTerm"
self.vterm = vterm
def get_math_representation(self):
return self.vterm.get_math_representation()+"("+super(VarPol, self).get_math_representation()+")"
t = VarTerm(2, "x", 3)
t
2 x^3
t.show()
p1 = VarPol( vterm=VarTerm(1,"x",3), first_node=Node(VarTerm(2,"y", 2), Node(VarTerm(5,"y"))))
p1.show()
p2 = VarPol(first_node=Node(VarTerm(7,"y",2)), vterm=VarTerm(1,"x",1))
p2.show()
p3 = VarPol(first_node=Node(p1, Node(p2)), vterm=VarTerm(1,"z", 2))
p3.show()
p4 = VarPol( vterm=VarTerm(1,"x",2), first_node=Node(VarTerm(5,"y", 1)))
p4.show()
p5 = VarPol( first_node=Node(p4, Node(VarTerm(4,"x",1))), vterm=VarTerm(1,"z",1))
p5.show()
p6 = VarPol( vterm=VarTerm(1,"x",3), first_node=Node(VarTerm(4,"y", 2)))
p6.show()
p7 = VarPol(first_node=Node(VarTerm(9,"y", 0), Node(VarTerm(8,"y",1))))
p7.show()
p8 = VarPol(first_node=Node(p3, Node(p5, Node(p6, Node(p7)))))
p8.show()
inspeccionemos el polinomio resultante
len(p8)
4
print(p8.vterm.get_math_representation())
for i in range(len(p8)):
print("term %d %s"%(i, p8[i].get_math_representation()))
term 0 z^2( x^3(2 y^2+5 y)+ x(7 y^2))
term 1 z( x^2(5 y)+4 x)
term 2 x^3(4 y^2)
term 3 (9+8 y)
k = p8[0]
print("vterm:", k.vterm.get_math_representation())
print("len: ", len(k))
for i in range(len(k)):
print("term %d %s"%(i, k[i].get_math_representation()))
k.show()
vterm: z^2
len: 2
term 0 x^3(2 y^2+5 y)
term 1 x(7 y^2)
k = p8[0][0]
print("vterm:", k.vterm.get_math_representation())
print("len: ", len(k))
for i in range(len(k)):
print("term %d %s"%(i, k[i].get_math_representation()))
k.show()
vterm: x^3
len: 2
term 0 2 y^2
term 1 5 y
## Ejercicios propuestos
obtén experimentalmente la complejidad computacional de cada método y arguméntalo.
implementa la suma de polinomios
VarPoldespués de hacer los ejercicios, cómo modificarías
Nodepara facilitar el acceso a índices negativos?