LAB 3.1 - TF model subclassing#
The labs require a tensorflow version lower than the default one used in Google Colab. Run the following cell to downgrade TensorFlow accordingly.
!wget -nc --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/2021.deeplearning/main/content/init.py
import init; init.init(force_download=False);
from local.lib.rlxmoocapi import submit, session
import inspect
session.LoginSequence(endpoint=init.endpoint, course_id=init.course_id, lab_id="L03.01", varname="student");
import numpy as np
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
import tensorflow as tf
import matplotlib.pyplot as plt
%matplotlib inline
%load_ext tensorboard
from sklearn.datasets import *
from local.lib import mlutils
tf.__version__
The tensorboard extension is already loaded. To reload it, use:
%reload_ext tensorboard
'2.19.0'
A multilayer perceptron
assuming \(n\) layers, the output at layer \(i\)
at the first layer
and the layer prediction is the output of the last layer:
with \(\text{activation}\) being an activation function, such as \(\text{sigmoid}(z) = \frac{1}{1+e^{-z}}\), \(\text{tanh}\), \(\text{ReLU}\), etc.
Cost (with regularization)
\(\lambda\) regulates the participation of the regularization terms. Given a vector or matrix \(\mathbf{T}\), its squared norm is denoted by \(||\mathbf{T}||^2 \in \mathbb{R}\) and it’s computed by squaring all its elements and summing them all up.
TASK 1: Model build#
Observe the class template below which is used to build a multilayer perceptron with a specific number of layers. In the constructor.
neuronsmust be a list of integers specifying the number of neurons of each hidden layer and the output layer.activationsmust be a list of strings specifying the activations of the neurons of each layer.
Both neurons and activations must have the same number of elements. Observe how in the class constructor (__init__) we check for this and transform the list of activation strings to actual TF funcions.
YOU MUST complete the build method in the class below so that self.W and self.b contain a list of tensors with randomly initialized weights for each layer. Create the weights by calling the self.add_weights function for each layer, both for the weights (add them to list self.W) and the biases (add them to list b). Call self.add_weights with parameters initializer='random_normal', trainable=True, dtype=tf.float32.
Note that the shape of the first layer weights are not known until the build method is called which is when the input_shape for the input data is known. For instance, the following invokations
>> mlp = MLP_class(neurons=[10,5,1], activations=["tanh","tanh", "sigmoid"])
>> mlp.build([None, 2])
>> print ("W shapes", [i.shape for i in mlp.W])
should produce the following output
W shapes [TensorShape([2, 10]), TensorShape([10, 5]), TensorShape([5, 1])]
b shapes [TensorShape([10]), TensorShape([5]), TensorShape([1])]
def MLP(neurons, activations, reg=0.):
from tensorflow.keras import Model
from tensorflow.keras.activations import relu, sigmoid, tanh, linear
import numpy as np
import tensorflow as tf
class MLP_class(Model):
def __init__(self, neurons, activations, reg=0.):
super().__init__()
self.activation_map = {"linear": linear, "relu": relu, "tanh":tanh, "sigmoid": sigmoid}
assert len(neurons)==len(activations), \
"must have the same number of neurons and activations"
assert np.all([i in self.activation_map.keys() for i in activations]), \
"activation string not recognized"
self.neurons = neurons
self.reg = reg
self.activations = [self.activation_map[i] for i in activations]
super().__init__()
def build(self, input_shape):
self.W = []
self.b = []
... # YOUR CODE HERE
return MLP_class(neurons, activations, reg)
test manually your code
mlp = MLP(neurons=[10,5,1], activations=["tanh","tanh", "sigmoid"])
mlp.build([None, 2])
print ("W shapes", [i.shape for i in mlp.W])
print ("b shapes", [i.shape for i in mlp.b])
Registra tu solución en linea
student.submit_task(namespace=globals(), task_id='T1');
Task 2: Model call#
Complete the call method below so that it computes the output of the configured MLP with the input X as
as described above. Use self.W, self.b and self.activations as constructed previously on the build and __init__ methods.
def MLP2(neurons, activations, reg=0.):
from tensorflow.keras import Model
from tensorflow.keras.activations import relu, sigmoid, tanh, linear
class MLP_class(Model):
def __init__(self, neurons, activations, reg=0.):
super().__init__()
self.activation_map = {"linear": linear, "relu": relu, "tanh":tanh, "sigmoid": sigmoid}
assert len(neurons)==len(activations), \
"must have the same number of neurons and activations"
assert np.all([i in self.activation_map.keys() for i in activations]), \
"activation string not recognized"
self.neurons = neurons
self.reg = reg
self.activations = [self.activation_map[i] for i in activations]
super().__init__()
def build(self, input_shape):
self.W = []
self.b = []
... # YOUR CODE HERE (copy from previous task )
@tf.function
def call(self, X):
a = ... # YOUR CODE HERE
return s
return MLP_class(neurons, activations, reg)
test manually your code, the following two cells must return the same value everytime you execute them. Observe your MLP will initialize to different random weights each time.
X = np.random.random(size=(4,2))
neurons = [3,2]
mlp = MLP2(neurons=[3,2], activations=["linear", "sigmoid"])
mlp(X)
sigm = lambda x: 1/(1+np.exp(-x))
W = [i.numpy() for i in mlp.W]
b = [i.numpy() for i in mlp.b]
sigm((X.dot(W[0])+b[0]).dot(W[1])+b[1])
Registra tu solución en linea
student.submit_task(namespace=globals(), task_id='T2');
Task 3: Loss function#
Complete the loss method below so that it computes the loss of the MLP given predictions y_pred (as the output of the network) and desired output y_true.
observe the regularization term \(\lambda\) which is stored as self.reg in your class.
For any weight or bias \(\mathbf{k}\), the expression \(\| \mathbf{k}\|^2_{mean}\) is the mean of all its elements squared.
def MLP3(neurons, activations, reg=0.):
from tensorflow.keras import Model
from tensorflow.keras.activations import relu, sigmoid, tanh, linear
class MLP_class(Model):
def __init__(self, neurons, activations, reg=0.):
super().__init__()
self.activation_map = {"linear": linear, "relu": relu, "tanh":tanh, "sigmoid": sigmoid}
assert len(neurons)==len(activations), \
"must have the same number of neurons and activations"
assert np.all([i in self.activation_map.keys() for i in activations]), \
"activation string not recognized"
self.neurons = neurons
self.reg = reg
self.activations = [self.activation_map[i] for i in activations]
super().__init__()
def build(self, input_shape):
self.W = []
self.b = []
... # YOUR CODE HERE (copy from previous task)
@tf.function
def call(self, X):
a = ... # YOUR CODE HERE (copy from previous task)
return s
@tf.function
def custom_loss(self, y_true, y_pred):
r = ... # YOUR CODE HERE
return ...
return MLP_class(neurons, activations, reg)
test manually your code, the following two cells must return the same value everytime you execute them. Observe your MLP will initialize to different random weights each time.
X = np.random.random(size=(4,2)).astype(np.float32)
y_true = np.random.randint(2, size=(len(X),1)).astype(np.float32)
neurons = [3,2]
mlp = MLP3(neurons=[3,1], activations=["linear", "sigmoid"], reg=0.2)
mlp.custom_loss(mlp(X), y_true).numpy()
WARNING:tensorflow:5 out of the last 6 calls to <function MLP3.<locals>.MLP_class.call at 0x7d11dcfabba0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has reduce_retracing=True option that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
np.float32(0.25332093)
sigm = lambda x: 1/(1+np.exp(-x))
W = [i.numpy() for i in mlp.W]
b = [i.numpy() for i in mlp.b]
y_pred = sigm((X.dot(W[0])+b[0]).dot(W[1])+b[1])
((y_pred-y_true)**2).mean() + mlp.reg * np.sum([(i**2).numpy().mean() for i in mlp.W+mlp.b])
np.float32(0.25332093)
Registra tu solución en linea
student.submit_task(namespace=globals(), task_id='T3');
Done!!#
now you can try your class with synthetic data
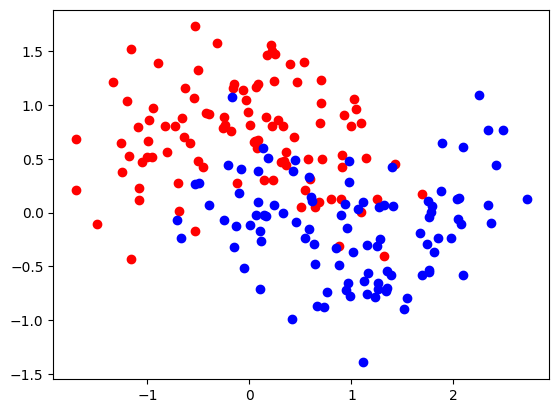
X, y = make_moons(200, noise=.35)
X, y = X.astype(np.float32), y.astype(np.float32).reshape(-1,1)
plt.scatter(X[:,0][y[:,0]==0], X[:,1][y[:,0]==0], color="red", label="class 0")
plt.scatter(X[:,0][y[:,0]==1], X[:,1][y[:,0]==1], color="blue", label="class 1")
<matplotlib.collections.PathCollection at 0x7d11c3910830>
create MLP and train!!
mlp = MLP3(neurons=[10,1], activations=["tanh","sigmoid"], reg=0.0)
mlp.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.1), loss=mlp.custom_loss,
metrics=[tf.keras.metrics.mae, tf.keras.metrics.binary_accuracy])
!rm -rf logs
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir="logs/no_regularization")
mlp.fit(X,y, epochs=400, batch_size=16, verbose=0,
callbacks=[tensorboard_callback])
<keras.src.callbacks.history.History at 0x7d11c3910530>
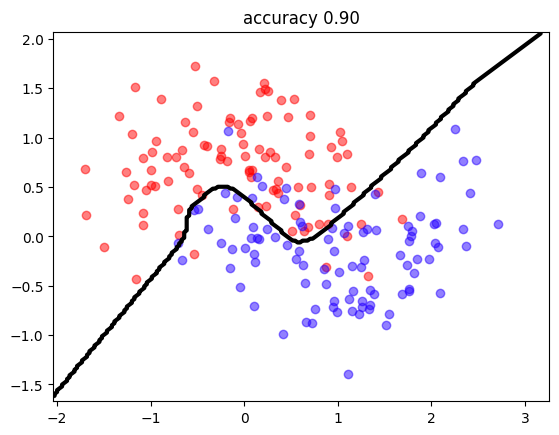
observe the accuracy and classification frontier
predict = lambda X: (mlp.predict(X)[:,0]>0.5).astype(int)
mlutils.plot_2Ddata_with_boundary(predict, X, y.reshape(-1));
plt.title("accuracy %.2f"%np.mean(predict(X)==y.reshape(-1)));
1250/1250 ━━━━━━━━━━━━━━━━━━━━ 1s 667us/step
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step
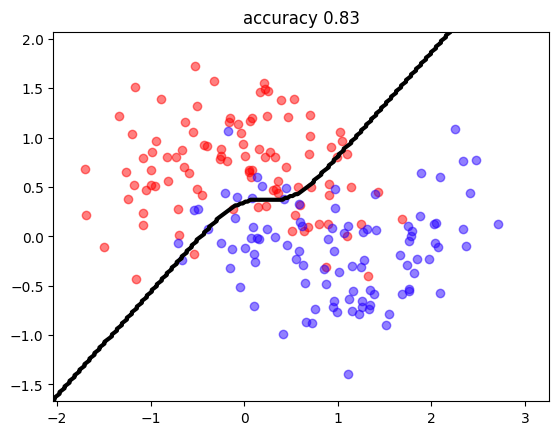
regularization must work!!!
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir="logs/with_regularization")
mlp = MLP3(neurons=[10,1], activations=["tanh","sigmoid"], reg=0.005)
mlp.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.1), loss=mlp.custom_loss,
metrics=[tf.keras.metrics.mae, tf.keras.metrics.binary_accuracy])
mlp.fit(X,y, epochs=400, batch_size=10, verbose=0, callbacks=[tensorboard_callback])
mlutils.plot_2Ddata_with_boundary(predict, X, y.reshape(-1))
plt.title("accuracy %.2f"%np.mean(predict(X)==y.reshape(-1)));
1250/1250 ━━━━━━━━━━━━━━━━━━━━ 1s 670us/step
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step
and inspect tensorboard
%load_ext tensorboard
%tensorboard --logdir logs

