LAB 06.01 - Clustering companies

!wget --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/ai4eng.v1/main/content/init.py
import init; init.init(force_download=False); init.get_weblink()

from local.lib.rlxmoocapi import submit, session
session.LoginSequence(endpoint=init.endpoint, course_id=init.course_id, lab_id="L06.01", varname="student");

Dataset

observe the following dataset with daily stock data from different companies

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import Image
%matplotlib inline

d = pd.read_csv("local/data/company-stock-movements-2010-2015-incl.csv.gz", index_col=0)
d.shape

(60, 963)

d.head()

	2010-01-04	2010-01-05	2010-01-06	2010-01-07	2010-01-08	2010-01-11	2010-01-12	2010-01-13	2010-01-14	2010-01-15	...	2013-10-16	2013-10-17	2013-10-18	2013-10-21	2013-10-22	2013-10-23	2013-10-24	2013-10-25	2013-10-28	2013-10-29
Apple	0.580000	-0.220005	-3.409998	-1.170000	1.680011	-2.689994	-1.469994	2.779997	-0.680003	-4.999995	...	0.320008	4.519997	2.899987	9.590019	-6.540016	5.959976	6.910011	-5.359962	0.840019	-19.589981
AIG	-0.640002	-0.650000	-0.210001	-0.420000	0.710001	-0.200001	-1.130001	0.069999	-0.119999	-0.500000	...	0.919998	0.709999	0.119999	-0.480000	0.010002	-0.279998	-0.190003	-0.040001	-0.400002	0.660000
Amazon	-2.350006	1.260009	-2.350006	-2.009995	2.960006	-2.309997	-1.640007	1.209999	-1.790001	-2.039994	...	2.109985	3.699982	9.570008	-3.450013	4.820008	-4.079986	2.579986	4.790009	-1.760009	3.740021
American express	0.109997	0.000000	0.260002	0.720002	0.190003	-0.270001	0.750000	0.300004	0.639999	-0.130001	...	0.680001	2.290001	0.409996	-0.069999	0.100006	0.069999	0.130005	1.849999	0.040001	0.540001
Boeing	0.459999	1.770000	1.549999	2.690003	0.059997	-1.080002	0.360000	0.549999	0.530002	-0.709999	...	1.559997	2.480003	0.019997	-1.220001	0.480003	3.020004	-0.029999	1.940002	1.130005	0.309998

5 rows × 963 columns

d.index

Index(['Apple', 'AIG', 'Amazon', 'American express', 'Boeing',
       'Bank of America', 'British American Tobacco', 'Canon', 'Caterpillar',
       'Colgate-Palmolive', 'ConocoPhillips', 'Cisco', 'Chevron',
       'DuPont de Nemours', 'Dell', 'Ford', 'General Electrics',
       'Google/Alphabet', 'Goldman Sachs', 'GlaxoSmithKline', 'Home Depot',
       'Honda', 'HP', 'IBM', 'Intel', 'Johnson & Johnson', 'JPMorgan Chase',
       'Kimberly-Clark', 'Coca Cola', 'Lookheed Martin', 'MasterCard',
       'McDonalds', '3M', 'Microsoft', 'Mitsubishi', 'Navistar',
       'Northrop Grumman', 'Novartis', 'Pepsi', 'Pfizer', 'Procter Gamble',
       'Philip Morris', 'Royal Dutch Shell', 'SAP', 'Schlumberger', 'Sony',
       'Sanofi-Aventis', 'Symantec', 'Toyota', 'Total',
       'Taiwan Semiconductor Manufacturing', 'Texas instruments', 'Unilever',
       'Valero Energy', 'Walgreen', 'Wells Fargo', 'Wal-Mart', 'Exxon',
       'Xerox', 'Yahoo'],
      dtype='object')

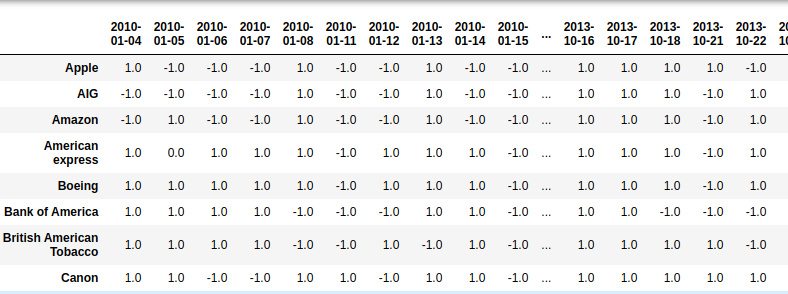
TASK 1: convert d into a signed dataframe

turn all values to 1 if >0 and -1 otherwise

the resulting dataset must look like the following image

HINT: use numpy.sign

Image("local/imgs/stock_signed.png")

def signed(d):
    result = ....
    return result

manually check your code

signed(d)

submit your code

student.submit_task(globals(), task_id="task_01");

Exercise 2: implement custom metric

the intuition is that we want our metric to reward sets of symbols moving in sync.

So, given a matrix:

1. for each column compute the max number of positions with equal value.

2. divide by the number of elements in the column

3. average the value for all columns

for instance, for the following matrix

m  = np.array([[-1,  1,  1, -1],
               [-1, -1,  1, -1],
               [-1, -1,  1,  1],
               [-1, -1, -1,  1],
               [-1,  1,  1, -1],
               [-1, -1,  1, -1]])

1. the number of positions of equal value for each column is 6,4,5,4

2. normalizing by the number of elements per column (6) is 1,0.6667,.8333,.6667

3. the mean of the previous result is about 0.792

complete the following function to compute this metric, assuming the input matrix m is a numpy array containing only values of -1 and 1

suggested strategy: loop over the columns, compute the number of 1’s and -1’s and keep whichever is grater in each column, divide by the length of m (you will have then one number per column), and take the average.

challenge 1: solve it with one line

challenge 2: solve it without a loop, but using the axis argument when using np.sum and np.max

def mean_sync_move(m):
    result = ...
    return result

manually check your code

mean_sync_move(m)

the following must return 1

mean_sync_move(np.ones((10,2)))

obtain the mean_sync_move of the full dataset AFTER converting it into signed. It should be around 0.72

mean_sync_move(signed(d).values)

submit your code

student.submit_task(globals(), task_id="task_02");

Task 3: Cluster the full dataset

complete the following function such that upon receiving a dataset:

• obtains the signed dataset

• uses sklearn KMeans to cluster the dataset with the given number of clusters (n_clusters)

• predicts the cluster number of each company

• for each cluster number:

  • filters the signed dataset so that it keeps the companies belonging to that cluster.

  • computes the mean_sync_move of the resulting filtered signed dataset.

your function must return a dataframe with one row per cluster containing

• the cluster number

• the number of companies in the cluster

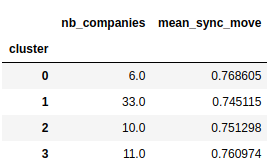
• the mean_sync_move of each cluster

for instance, for 4 clusters your resulting dataframe should look like the following one. The cluster numbers might be in a different order, but the index and the columns MUST be as illustrated.

important: use random_state=2 when creating the KMeans instance.

Image(filename='local/imgs/labclusters.png')

from sklearn.cluster import KMeans

def cluster_dataset(d, n_clusters):
    
    def signed(d):
        return ... # your code here
    
    def mean_sync_move(m):
        return ... # your code here
    
    d = signed(d)
    
    c = KMeans(....)
    y = c.fit_predict(...)
    r = pd.DataFrame(...., columns=["cluster", "nb_companies", "mean_sync_move"])    
   
    r.index = r.cluster.values.astype(int)
    r.index.name = "cluster"
    
    del(r["cluster"])
    return r

cluster_dataset(d, n_clusters=4)

submit your code

student.submit_task(globals(), task_id="task_03");

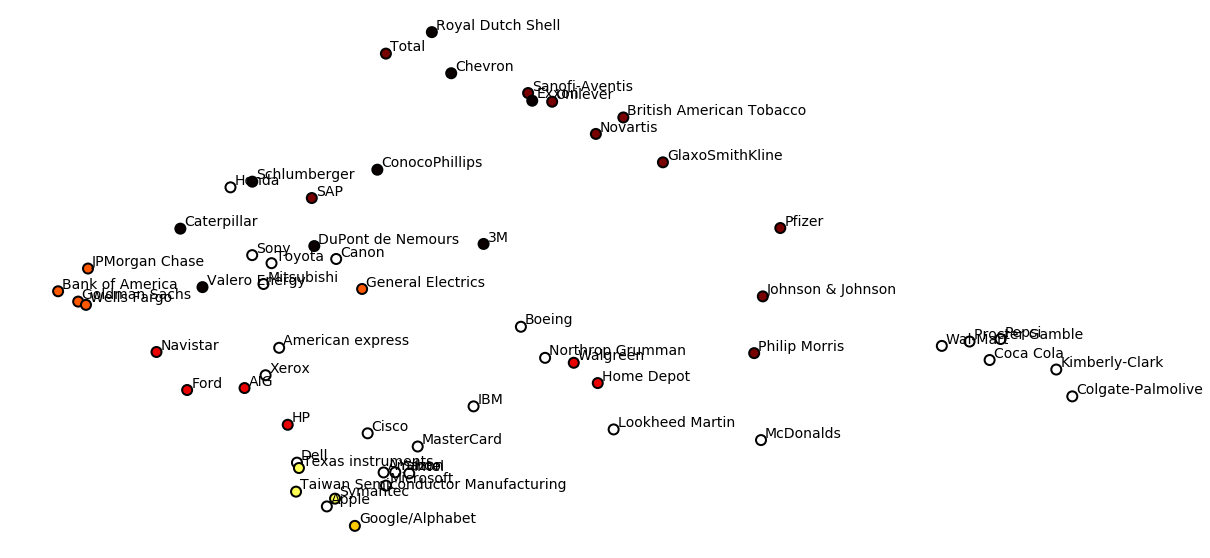
Compare with PCA

we apply PCA with 2 components to +1/-1 dataset and visualize clusters

from sklearn.decomposition import PCA

n_clusters = 7

X = PCA(n_components=2).fit_transform(signed(d).values)
y = KMeans(n_clusters=10).fit_predict(signed(d).values)

cmap = plt.cm.hot
plt.figure(figsize=(20,10))
plt.scatter(X[:,0], X[:,1], color=cmap((y*255./(n_clusters-1)).astype(int)), s=100, edgecolor="black", lw=2)
for i in range(len(d)):
    name = d.index[i]
    plt.text(X[i,0]+.1, X[i,1]+.1,d.index[i], fontsize=14)
plt.axis("off");

---

---

Other suggested exercises

Try the following exercises from O’Reilly’s Python Data Science Handbook, and its associated Notebook Repository at Chapter about Clustering :

• Clustering, Exercise 1: k-Means on Digits

• Clustering, Exercise 2: k-Means for Color Compression