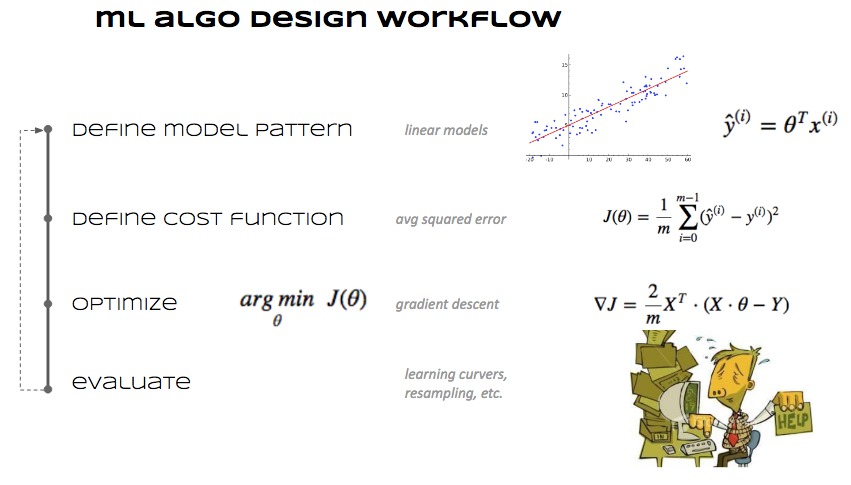
07.02 - DESIGN ML ALGORITHMS

!wget --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/ai4eng.v1/main/content/init.py
from init import init; init(force_download=False)

Cómo se diseña un algoritmo ML

1. Elegir de qué parámetros depende una predicción \(\rightarrow\) se define cómo es un modelo.

2. Definir una función que mida el error de la predicción.

3. Determinar qué valores de los parámetros minimizan el error de predicción.

## KEEPOUTPUT
from IPython.display import Image
Image(filename='local/imgs/mldesign.jpg', width=800)

Ejemplo

Los Trilotrópicos son insectos imaginarios que viven en las latitudes tropicales. Conocer su densidad de escamas es muy importante para poder saber qué insecticida aplicar. Pero es muy costoso contar las escamas.

Creemos que existe una relación entre la longitud y la densidad de escamas y queremos un modelo que prediga la densidad a partir de la longitud.

Esto es una tarea de regresión, ya que la predicción \(\in \mathbb{R}\)

Tenemos datos anotados (alguien contó las escamas de unos cuantos trilotrópicos) \(\rightarrow\) estamos ante una tarea de aprendizaje supervisado

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.optimize import minimize
%matplotlib inline

## KEEPOUTPUT
d = pd.read_csv("local/data/trilotropicos.csv")
print (d.shape)
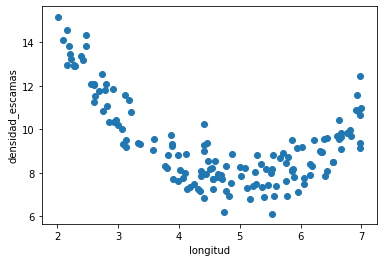
plt.scatter(d.longitud, d.densidad_escamas)
plt.xlabel(d.columns[0])
plt.ylabel(d.columns[1]);

(150, 2)

1. Elegimos la forma del modelo

Entrada

• \(x^{(i)}\): longitud del trilotrópico \(i\)

Salida esperada

• \(y^{(i)}\): densidad de escamas del trilotrópico \(i\)

**Predicción ** \(\rightarrow\) decidimos que nuestro modelo tiene la siguiente forma

• \(\hat{y}^{(i)} = \theta_0 + \theta_1 x^{(i)}\)

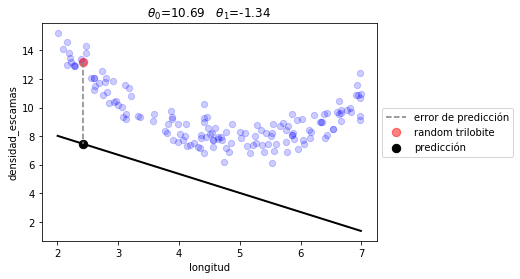
La siguiente es una posible combinación de \(\theta_0\) y \(\theta_1\) seleccionada aleatoriamente. Ejecútalo varias veces para entender el error.

def linear_prediction(t, x):
    t0,t1 = t
    return t0 + t1*x

## KEEPOUTPUT
t0 = np.random.random()*5+10
t1 = np.random.random()*4-3
p = d.iloc[np.random.randint(len(d))]
long = p.longitud
dens = p.densidad_escamas
print ("RANDOM t0 = %.3f, t1 = %.3f"%(t0,t1))
print ("\nlong = %.3f\ndens = %.3f"%(long, dens))
print ("\npred = %.3f (WITH RANDOM t0 t1)"%linear_prediction([t0,t1], long) )

RANDOM t0 = 10.693, t1 = -1.336

long = 4.770
dens = 7.159

pred = 4.320 (WITH RANDOM t0 t1)

## KEEPOUTPUT
def plot_model(t, prediction):
    xr = np.linspace(np.min(d.longitud), np.max(d.longitud), 100)
    plt.scatter(d.longitud, d.densidad_escamas, s=40, alpha=.2, color="blue", label="")
    plt.plot(xr,prediction(t,xr), lw=2, color="black")
    plt.title("   ".join([r"$\theta_%d$=%.2f"%(i, t[i]) for i in range(len(t))]));

    p = d.iloc[np.random.randint(len(d))]
    pred = prediction(t, p.longitud)
    plt.plot([p.longitud, p.longitud], [p.densidad_escamas, pred], ls="--", color="gray", label=u"error de predicción")
    plt.scatter(p.longitud, p.densidad_escamas, s=70, alpha=.5, color="red", label="random trilobite")
    plt.scatter(p.longitud, pred, s=70, alpha=1., color="black", label=u"predicción")
    plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))

    plt.xlabel(d.columns[0])
    plt.ylabel(d.columns[1]);
    

plot_model([t0,t1], linear_prediction)

2. Definimos una medida de error

Para un dato cualquiera \((i)\) $\( \begin{align} err^{(i)} &= (\hat{y}^{(i)}-y^{(i)})^2\\ &=(\theta_0 + \theta_1 x^{(i)} - y^{(i)})^2 \end{align}\)$

Para todo el dataset

\[J(\theta_0, \theta_1) = \frac{1}{m} \sum_{i=0}^{m-1}(\theta_0 + \theta_1 x^{(i)} - y^{(i)})^2\]

si asumimos que

• \(\overline{\theta} = [\theta_0, \theta_1]\)

• \(\mathbf{x}^{(i)} = [1, x^{(i)}]\)

entonces podemos escribir de manera más compacta la expresión anterior:

\[J(\overline{\theta}) = \frac{1}{m} \sum_{i=0}^{m-1}(\overline{\theta} \dot \; \mathbf{x}^{(i)} - y^{(i)})^2\]

def J(t, x, y, prediction):
    return np.mean( (prediction(t,x)-y)**2)
    

J([t0,t1], d.longitud, d.densidad_escamas, linear_prediction)

27.289016766830752

3. Obtenemos los parámetros que minimizan el error de predicción

observa cómo usamos un algoritmo genérico de optimización

## KEEPOUTPUT
r1 = minimize(lambda t: J(t, d.longitud, d.densidad_escamas, linear_prediction), np.random.random(size=2))
r1

      fun: 2.7447662570802733
 hess_inv: array([[ 5.56677384, -1.08863729],
       [-1.08863729,  0.233761  ]])
      jac: array([-3.87430191e-07, -2.65240669e-06])
  message: 'Optimization terminated successfully.'
     nfev: 36
      nit: 8
     njev: 9
   status: 0
  success: True
        x: array([12.68999889, -0.7180593 ])

## KEEPOUTPUT
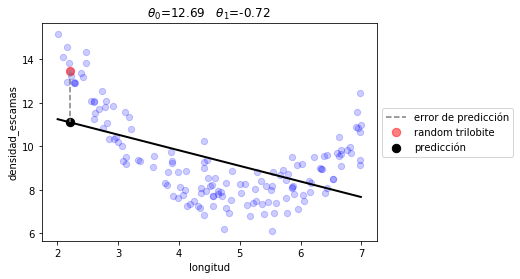
plot_model(r1.x, linear_prediction)
print ("error total %.2f"%(J(r1.x, d.longitud, d.densidad_escamas, linear_prediction)))

error total 2.74

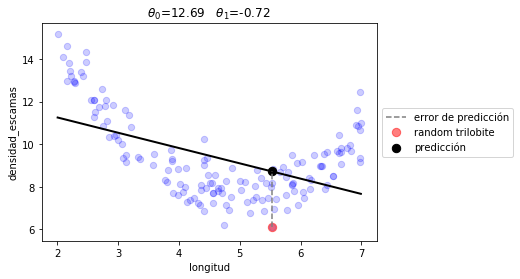
fíjate que son los mismos valores que la regresión lineal clásica

## KEEPOUTPUT
from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(d.longitud.values.reshape(-1,1), d.densidad_escamas)
t0, t1 = lr.intercept_, lr.coef_
print (t0, t1)
plot_model([t0,t1], linear_prediction)
print ("error total %.2f"%(J([t0, t1], d.longitud, d.densidad_escamas, linear_prediction)))

12.689998055222224 [-0.71805908]
error total 2.74

WARN!! Black box optimization can only be used for VERY SIMPLE models

in ML normally you have to:

• compute the partial derivatives of the parameters of the cost function

• use optimizers specially designed for ML

Otra forma de modelo

esta vez con tres parámetros y un término cuadrático

\[\hat{y}^{(i)} = \theta_0 + \theta_1 x^{(i)} + \theta_2 (x^{(i)})^2\]

def quad_prediction(t, x):
    t0,t1,t2 = t
    return t0 + t1*x + t2*x**2

r2 = minimize(lambda t: J(t, d.longitud, d.densidad_escamas, quad_prediction), np.random.random(size=3))
r2

      fun: 0.5533076730536329
 hess_inv: array([[ 50.71906017, -23.19602691,   2.42715945],
       [-23.19602691,  11.05458208,  -1.18794883],
       [  2.42715945,  -1.18794883,   0.1304395 ]])
      jac: array([-2.98023224e-08,  2.23517418e-08,  2.23517418e-07])
  message: 'Optimization terminated successfully.'
     nfev: 80
      nit: 14
     njev: 16
   status: 0
  success: True
        x: array([26.75881715, -7.61054361,  0.75701901])

## KEEPOUTPUT
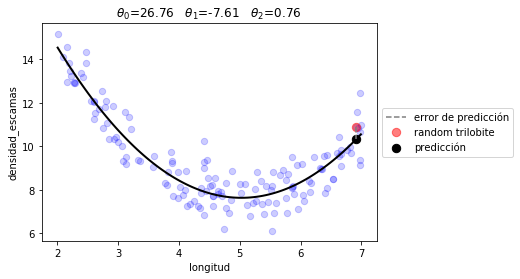
plot_model(r2.x, quad_prediction)
print ("error total %.2f"%(J(r2.x, d.longitud, d.densidad_escamas, quad_prediction)))

error total 0.55

observa como indirectamente hacemos lo mismo con la regresión lineal de sklearn añadiendo explícitamente una columna con la longitud al cuadrado

lr = LinearRegression()
lr.fit(np.r_[[d.longitud.values, d.longitud.values**2]].T, d.densidad_escamas)
t0, (t1, t2) = lr.intercept_, lr.coef_
t0, t1, t2

(26.75883713364987, -7.61055346692438, 0.7570201016172385)