06.02 - PCA#
!wget --no-cache -O init.py -q https://raw.githubusercontent.com/rramosp/ai4eng.v1/main/content/init.py
import init; init.init(force_download=False); init.get_weblink()
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
consulta A Tutorial on Principal Component Analysis para una decripción intuitiva y detallada de PCA y SVD
Intuición#
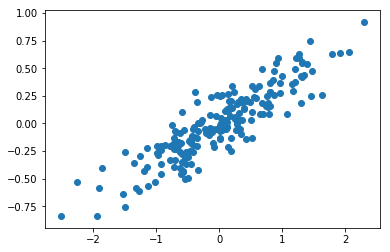
tenemos los siguientes datos 2D y nos gustaría encontrar una proyección en 1D que preserve la máxima cantidad de variabilidad.
np.random.seed(1)
X = np.dot(np.random.random(size=(2, 2)), np.random.normal(size=(2, 200))).T+10
# center data on 0,0
X=X-np.mean(X, axis=0)
print (X.shape)
plt.scatter(X[:,0], X[:,1])
(200, 2)
<matplotlib.collections.PathCollection at 0x7fa907e03890>
recuerda que la proyección de un vector \(\vec{x}\) en otro vector \(\vec{v}\) (consulta here) viene dada por:
donde \(c\) es el tamaño de la proyección de \(\vec{x}\) sobre \(\vec{v}\)
inspeccionamos algunas proyecciones#
plt.figure(figsize=(15,3))
unit_vector = lambda angle: np.array([np.cos(angle), np.sin(angle)])
for i in range(3):
plt.subplot(1,3,i+1)
angle = np.random.random()*np.pi*2 if i!=0 else 1.8
v = unit_vector(angle)
c = X.dot(v.reshape(-1,1))/(np.linalg.norm(v)**2)
Xp = np.repeat(v.reshape(-1,2),len(X),axis=0)*c
plt.scatter(X[:,0], X[:,1], color="blue", alpha=.5, label="original data")
plt.scatter(Xp[:,0], Xp[:,1], color="red", alpha=.5, label="projected data")
plt.axvline(0, color="gray")
plt.axhline(0, color="gray")
plt.plot([0,v[0]], [0,v[1]], color="black", lw=3, label="projection vector")
plt.axis('equal')
plt.ylim(-2,2)
plt.title("$\\alpha$=%.2f rads, proj std=%.3f"%(angle, np.std(c)))
if i==2:
plt.legend(loc="center left", bbox_to_anchor=(1.01,.5))
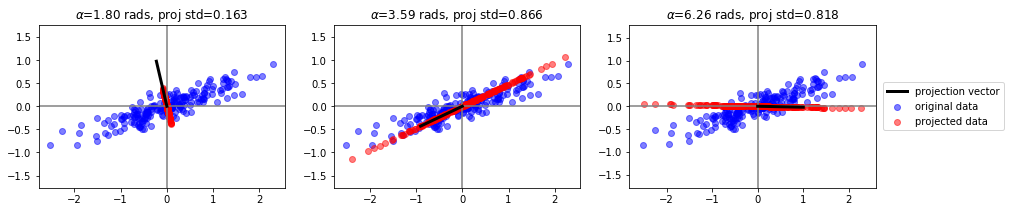
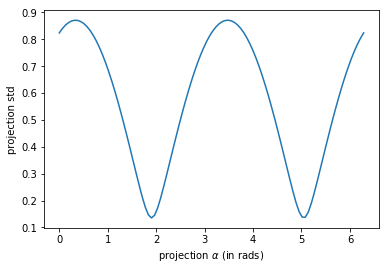
encontremos las proyecciones con mayor y menor std por fuerza bruta#
def get_maxmin_projections(X):
stds = []
angles = np.linspace(0,np.pi*2, 100)
for a in angles:
v = np.array([np.cos(a), np.sin(a)])
c = X.dot(v.reshape(-1,1))/(np.linalg.norm(v)**2)
stds.append(np.std(c))
v2 = unit_vector(angles[np.argmin(stds)])
v1 = unit_vector(angles[np.argmax(stds)])
return angles, stds, v1, v2
angles, stds, v1, v2 = get_maxmin_projections(X)
plt.plot(angles, stds)
plt.xlabel("projection $\\alpha$ (in rads)")
plt.ylabel("projection std")
Text(0,0.5,'projection std')
plt.scatter(X[:,0], X[:,1], color="blue", alpha=.5, label="original data")
plt.axvline(0, color="gray")
plt.axhline(0, color="gray")
plt.plot([0,v1[0]], [0,v1[1]], color="black", lw=5, label="max std projection vector")
plt.plot([0,v2[0]], [0,v2[1]], color="black", ls="--", lw=2, label="min std projection vector")
plt.axis('equal')
plt.ylim(-2,2)
plt.legend(loc="center left", bbox_to_anchor=(1.01,.5))
<matplotlib.legend.Legend at 0x7fa907afc450>
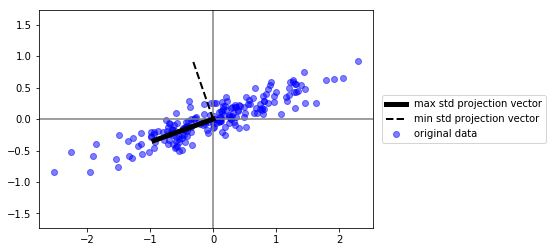
estos son los componentes principales!! observa que su dimensionalidad es la misma que los datos originales
esto es lo que PCA nos da
from sklearn.decomposition import PCA
pca = PCA(n_components=1)
pca.fit(X)
print ("sklearn PCA components")
print (pca.components_)
print ("brute force components")
print (v1)
print (v2)
sklearn PCA components
[[-0.94446029 -0.32862557]]
brute force components
[-0.93969262 -0.34202014]
[-0.32706796 0.94500082]
c = pca.transform(X)
print (c.shape)
c
(200, 1)
array([[ 6.76769235e-01],
[-1.07121393e+00],
[ 7.27912364e-01],
[ 2.30964136e+00],
[ 6.30052323e-01],
[ 1.02448887e+00],
[ 7.77183507e-01],
[-1.39656414e+00],
[-2.91049874e-01],
[ 1.88864221e+00],
[-7.11544293e-01],
[ 6.38884130e-01],
[ 5.48059617e-01],
[-2.19312436e-01],
[-3.87789490e-01],
[ 7.15219956e-01],
[-1.08373816e+00],
[-2.99917403e-01],
[-7.96849021e-01],
[-8.12568346e-01],
[-1.54018281e+00],
[-2.52920476e-01],
[ 6.26464454e-01],
[-1.61007571e+00],
[ 5.04240563e-01],
[ 5.53935753e-01],
[ 6.81911252e-01],
[-2.00157228e-02],
[ 1.13550833e-01],
[ 2.92286085e-02],
[-2.14393483e-01],
[-1.03406124e+00],
[ 3.88635004e-01],
[ 9.96727811e-01],
[ 1.39223653e+00],
[ 4.57043694e-01],
[ 6.81839901e-01],
[-9.05233246e-01],
[ 4.94316334e-01],
[ 6.22411280e-01],
[ 3.26088548e-01],
[ 4.52560386e-01],
[ 6.81840663e-01],
[-2.44832816e-01],
[-5.27149562e-01],
[-4.51448737e-01],
[-1.42864453e+00],
[ 8.05233004e-01],
[ 1.81049742e-01],
[ 3.49039347e-01],
[ 2.65803583e+00],
[-1.34272221e+00],
[-1.73026340e-01],
[ 6.13676729e-01],
[-1.89940741e+00],
[-7.93074429e-01],
[-4.17072486e-01],
[ 1.54913526e-01],
[ 2.44646603e-01],
[ 7.26337140e-01],
[-7.91592424e-01],
[ 4.39666794e-01],
[-2.66630687e-01],
[-8.77131636e-01],
[-6.37447634e-01],
[-7.72982393e-01],
[-1.04616382e+00],
[ 1.15209837e+00],
[-5.26661400e-02],
[-9.74296354e-01],
[-6.24348505e-01],
[-1.00475074e+00],
[ 5.89973268e-01],
[ 1.50344054e+00],
[ 1.27433349e+00],
[-1.25658172e+00],
[ 1.37852445e-01],
[-1.36126475e+00],
[ 7.27518820e-01],
[ 4.50501231e-01],
[-1.17577071e-01],
[-8.49638130e-01],
[-9.51657336e-02],
[-1.81175961e-01],
[ 2.81596080e-01],
[-2.56560634e-01],
[ 8.52804745e-01],
[-4.77688980e-01],
[-2.96471868e-01],
[ 1.68108524e-03],
[-2.05727542e-01],
[ 8.12610001e-01],
[-7.06157363e-02],
[ 2.31690062e-01],
[-1.59605923e-01],
[-5.98727081e-01],
[ 1.01944512e+00],
[-7.01462226e-01],
[-1.40420099e+00],
[ 6.94997907e-01],
[ 5.18636606e-01],
[ 4.83061626e-01],
[ 6.79198052e-01],
[-1.30170017e+00],
[-2.71805220e-01],
[ 9.47603686e-01],
[-3.49630397e-01],
[ 4.85113462e-01],
[-3.04715098e-01],
[-3.31839520e-01],
[-1.38578436e+00],
[ 8.84502948e-01],
[-2.47084475e+00],
[-9.56899804e-02],
[-4.64806358e-01],
[ 7.06669625e-01],
[ 1.54312708e-01],
[ 5.45819213e-01],
[ 1.46023727e-01],
[ 9.57253276e-01],
[-6.91815248e-01],
[-1.00443516e-01],
[ 2.77924488e-01],
[-1.20207491e+00],
[-6.04953108e-02],
[-1.03273685e+00],
[ 6.88215760e-01],
[-1.21050656e+00],
[-2.40052449e-01],
[-6.06855334e-01],
[ 1.29217575e+00],
[-1.03282074e-01],
[-1.41361475e+00],
[ 7.57783205e-01],
[ 1.41360423e+00],
[ 1.99564613e+00],
[ 1.66865955e+00],
[ 1.66032125e+00],
[ 4.24742508e-01],
[-9.26445715e-01],
[ 3.28504629e-02],
[-5.17521702e-01],
[-9.24887775e-02],
[-3.05962249e-02],
[ 1.30795754e-01],
[-7.74659629e-02],
[-4.20826569e-01],
[ 6.78334448e-01],
[-6.35104074e-01],
[ 2.72075594e-01],
[-2.26801066e-01],
[-1.45908094e+00],
[ 4.03275391e-01],
[ 4.88618199e-01],
[-3.77797862e-02],
[ 2.25514691e-01],
[ 3.73320407e-01],
[ 9.96559672e-01],
[ 6.68655132e-01],
[-3.09207055e-01],
[ 1.44746288e+00],
[-1.27674147e-01],
[ 1.95898129e-02],
[-4.68331172e-01],
[-7.59794861e-01],
[ 2.11566325e+00],
[-1.28843614e+00],
[ 5.24455206e-01],
[ 2.68082969e-01],
[ 4.06271559e-02],
[-1.63087335e+00],
[ 4.50273668e-01],
[-1.41736985e+00],
[-3.20579341e-01],
[-2.16095416e+00],
[ 7.55938440e-01],
[ 1.13147728e+00],
[-4.01022769e-01],
[-1.33261395e-01],
[-1.20765775e-01],
[ 1.03185993e+00],
[-1.29878689e-01],
[-4.08011754e-01],
[ 4.17084437e-01],
[-1.00930809e-01],
[ 7.22839507e-02],
[ 6.47903117e-01],
[ 4.74689466e-01],
[ 6.85499472e-01],
[-1.49366216e+00],
[-3.49297457e-01],
[-7.79713261e-01],
[ 5.67446775e-01],
[ 5.18831382e-02],
[ 1.25350822e+00],
[-8.53016941e-01],
[-2.61547685e-01],
[-2.02667441e+00],
[ 1.20688282e+00],
[-3.53816725e-01]])
pero de modo mucho más eficiente
%timeit pca.fit(X)
144 µs ± 2.69 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
%timeit get_maxmin_projections(X)
3.1 ms ± 62.1 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
we can use the largest component to reduce our data from 2D to 1D#
podemos usar el componente mayor para reducir la dimensionalidad de nuestros datos de 2D a 1D#
observa que:
donde:
\(\mathbf{X}\) son nuestros datos
\(\mathbf{V}\) es el vector de componentes seleccionados
\(\mathbf{X_t}\) son los datos transformados
así que nos estamos restringiendo a transformaciones linealer (rotaciones y escalado)
pca = PCA(n_components=1)
pca.fit(X)
Xt = pca.transform(X)[:,0]
plt.scatter(X[:,0], X[:,1], color="blue", alpha=.5, label="$\mathbf{X}$: original data")
plt.scatter(Xt, [0]*len(Xt), color="red", alpha=.5, label="$\mathbf{X_t}$: reduced data")
plt.axis("equal");
plt.legend(loc="center left", bbox_to_anchor=(1.01,.5))
<matplotlib.legend.Legend at 0x7fa905b33650>
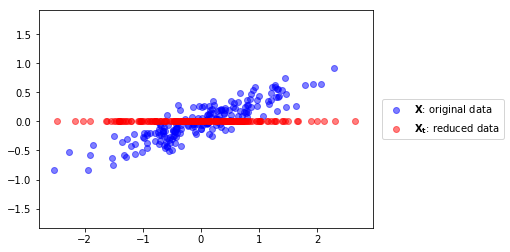
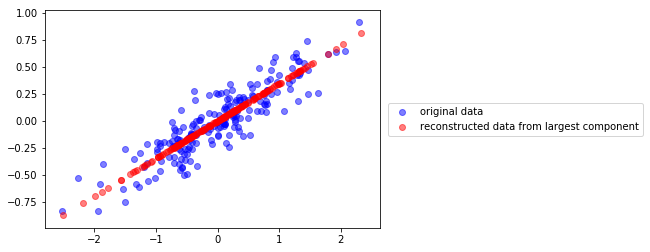
y podemos también recontruir los datos 2D después de la transformación
v0 = pca.components_[0]
c = X.dot(v0)
Xr = np.r_[[i*v0 for i in c]]
plt.scatter(X[:,0], X[:,1], color="blue", alpha=.5, label="original data")
plt.scatter(Xr[:,0], Xr[:,1], color="red", alpha=.5, label="reconstructed data from largest component")
plt.legend(loc="center left", bbox_to_anchor=(1.01,.5))
<matplotlib.legend.Legend at 0x7fa907c51d90>